補記・訂正
第2章
| 27頁11行目 |
50番目の51番目の中央 |
50番目と51番目の間が中央 |
|
|
|
|
|
第3章
| 45頁コードブロック3.4, 46頁図3.3 |
2つ目の要素がFeature
Onlyで3つ目の要素がDisplay Only |
2つ目の要素がDisplay
Onlyで3つ目の要素がFeature Only |
＊下記コードを参照 |
| 54頁本文1行目 |
モデル1の修正済み決定係数は0.268 |
モデル1の調整済み決定係数は0.266 |
直上で示した出力結果の調整済みでない決定係数の値となっているので訂正 |
| 54頁本文3行目 |
モデル2の修正済み決定係数は0.738 |
モデル2の調整済み決定係数は0.736 |
直上で示した出力結果の調整済みでない決定係数の値となっているので訂正 |
| 55頁本文1-2行目 |
モデル3の修正済み決定係数は0.739 |
モデル3の調整済み決定係数は0.739 |
|
|
|
|
|
- 45頁コードブロック3.4（メインページのコードも訂正済）
#-3.4--------------------------------------------------------------------------#
# 訂正前（教科書に掲載）
#boxplot(Sales / 1000 ~ Display + Feature,
# names = c(
# "No Feature & No Display", "Feature Only",
# "Display Only", "Feature & Display"),
# ylab = "Sales (1000JPY)", data = data_chap3)
# 訂正後
boxplot(Sales / 1000 ~ Display + Feature,
names = c(
"No Feature & No Display", "Display Only",
"Feature Only", "Feature & Display"),
ylab = "Sales (1000JPY)", data = data_chap3)
- 補記
- 第3章データについて、目的変数は「JPY（売上げ金額）」とありますが、「売上げ数量（リットルなど）」として解釈していただく方がモデルとしては適切ですので、適宜読み替えてください。
- p52～p53の尤度比検定について、モデル１の変数\(x_1\)に含まれている変数はすべてモデル２の変数\(x_2\)にも含まれている必要があります。
第4章
| 61頁19行目 |
これを\(y_t\)として |
これを\(y_{tA}\)として |
|
| 63頁8行目 |
上回る確率を解釈する |
上回る確率と解釈する |
|
| 64頁7行目 |
\(e_{t}\)に第1種極値分布を仮定した |
\(e_{t}\)にロジスティック分布を仮定した |
補記を参照 |
| 67頁コードブロック4.5 |
5列目－4列目 |
4列目－5列目 |
＊下記コードを参照 |
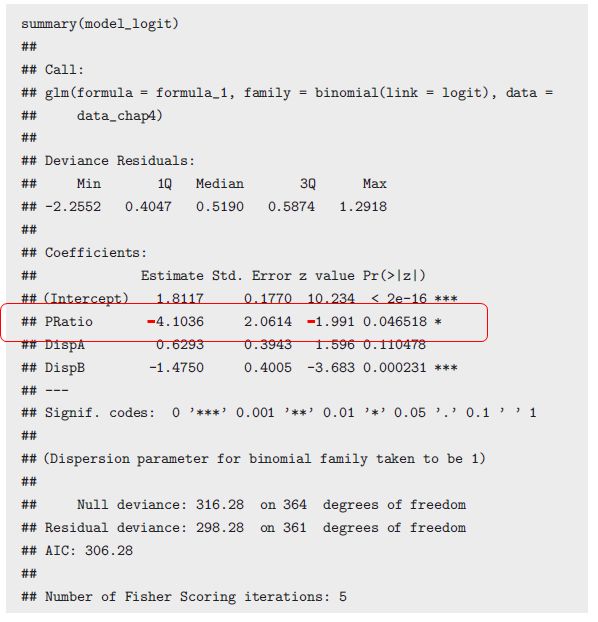
| 68頁コードブロック4.8 |
PRatioの符号が正 |
PRatioの符号が負 |
＊下記画像を参照
＊67頁コードブロック4.5を修正すると結果の符号が逆転する |
| 69頁コードブロック4.9 |
PRatioの符号が正 |
PRatioの符号が負 |
＊下記画像を参照
＊67頁コードブロック4.5を修正すると結果の符号が逆転する |
| 71頁6行目箇条書き2 |
ブランドBの市場シェアは低下する． |
ブランドAの市場シェアは低下する． |
|
| 73頁8行目 |
得れる結果が0か1なので |
得られる結果が0か1なので |
|
| 75頁表4.1 |
上段が「閾値=0.5」
下段が「閾値=市場シェア」 |
上段が「閾値=市場シェア」
下段が「閾値=0.5」 |
|
|
|
|
|
- 67頁コードブロック4.5（メインページのコードも訂正済）
#-4.5--------------------------------------------------------------------------#
# 訂正前（教科書に掲載）
#data_chap4["PRatio"] <- log(data_chap4[,5]) - log(data_chap4[,4])
# 訂正後
data_chap4["PRatio"] <- log(data_chap4[,4]) - log(data_chap4[,5])
- 68頁コードブロック4.8
- 68頁コードブロック4.9
- 補記
- 64頁7行目について、\(e_{tA}\)および\(e_{tB}\)に第1種極値分布を仮定すると、その差\(e_{t} =
e_{tB}-e_{tA}\)はロジスティック分布となります(Train
2009, p34-35)。\(e_{tA}\)および\(e_{tB}\)に平均0、分散0.5の正規分布を仮定すると、その差\(e_{t} =
e_{tB}-e_{tA}\)は標準正規分布となります（再生性）。
- 73頁表について、表側が「予測」、表頭が「実現」となっています。
本文中の説明およびコードでは齟齬はありませんが、表側に「実現」、表頭に「予測としている文献も多いのでここに補記します。75頁表4.1についても同様です。
- 参考文献
- Train, K. E. (2009). Discrete choice methods with simulation 2nd
edition. Cambridge university press.
第5章
| 90頁コードブロック5.5 |
オプション「chioce = “y”」 |
不要 |
＊下記コードを参照 |
| 91頁8行目 |
文中式 |
|
＊下記式を参照
＊表記ブレのため記載 |
|
|
|
|
- 90頁コードブロック5.5（メインページのコードも訂正済）
#-4.5--------------------------------------------------------------------------#
# 訂正前（教科書に掲載）
# オプション「choice」がスペルミスで無効になっているため、このままでも動作は正常
# ただし、「choice」に修正するとエラー
data_mlogit <- mlogit.data(data_chap5, varying = 4:23,
shape = "wide", chioce = "y")
# 訂正後
data_mlogit <- mlogit.data(data_chap5, varying = 4:23,
shape = "wide")
- 91頁8行目
- 誤：\(v_{ij} = \beta_{0j} + Price_{ij}
\gamma_{1}+ Disp_{ij} \gamma_{2}+ Feat_{ij}\gamma_{3} + FeatDisp_{ij}
\gamma_{4}\)
- 正：\(v_{ij} = \beta_{0j} + \gamma_{1}
Price_{ij} + \gamma_{2} Disp_{ij} + \gamma_{3} Feat_{ij} + \gamma_{4}
FeatDisp_{ij}\)
第6章
| 97頁表6.1 |
顧客の性別（女性=0, 男性=1） |
顧客の性別（女性=1, 男性=0） |
|
| 97頁5行目 |
女性=0, 男性=1のダミー変数 |
女性=1, 男性=0のダミー変数 |
|
| 115頁5行目 |
所属する確率が低いことがわかります． |
所属しにくいという解釈ができます． |
|
|
|
|
|
第7章
| 128頁16行目 |
(7.18)の右辺の第2項は標本選択バイアス |
(7.17)の右辺の第2項は標本選択バイアス |
|
| 132頁2行目 |
\(i\)のによってその値は |
\(i\)によってその値は |
|
第8章
| 149頁24行目 |
分散は\((\mu+\mu^2)/\theta\) |
分散は\(\mu+\mu^2/\theta\) |
|
| 150頁10行目 |
\(\theta\)は\(\beta\)から構成されますが |
\(\theta\)は\(\mu\)から構成され，\(\mu\)は\(\beta\)の関数になりますが |
分かりにくい表現だったので補足 |
| 154頁24行目 |
\(x_t'
\beta\)に加えて\(z_t' \gamma\)も推定 |
\(x_t'
\beta\)に加えて\(w_t' \gamma\)も推定 |
|
|
|
|
|
第9章
| 161頁9行目 |
分析対象の1,000台 |
分析対象の1,010台 |
|
| 169頁式(9.9) |
\(L(\beta)=\)\(\prod_{i1}^{N}\)(略) |
\(L(\beta)=\)\(\prod_{i=1}^{n}\)(略) |
|
| 171頁2行目 |
オートマチック車または |
マニュアル車または |
|
| 171頁式(9.12) |
\(\psi(x_i)=\)\(\exp(x_i'\beta)\) |
\(\psi(x_i)=\)\(\exp(- x_i'\beta)\) |
|
| 175頁2-3行目 |
オートマチック車がマニュアル車よりも |
マニュアル車がオートマチック車よりも |
|
|
|
|
|
- 補記
- 169頁式(9.9)(9,10)、171頁式(9.21)で使われている\(d_i\)は「\(i\)番目のデータが打ち切りデータであれば0をとり、そうでなければ\(1\)をとるダミー変数」になります。165頁で定義されている\(d_j\)とは異なるので注意してください。
第11章
| 206頁パス図 |
LUAT1～3へのパスのパラメータ\(b_{11},b_{12},b_{13}\) |
LUAT1～3へのパスのパラメータ\(b_{11},b_{21},b_{31}\) |
|
| 196頁14行目 |
理系学力の実が影響を |
理系学力のみが影響を |
|
| 198頁16行目 |
確認的因子分析を |
探索的因子分析を |
|
| 202頁2行目 |
算出方法がありまますが |
算出方法がありますが |
|
| 209頁11行目 |
得点を\(X_{ik}\)とおくと |
得点を\(X_{ik}\)とおき |
|
| 211頁8行目 |
計算の仮定を明確に |
計算の過程を明確に |
|
| 211頁3行目 |
誤差分散\(\varepsilon_k\)は |
誤差分散\(\sigma_k^2\)は |
|
| 212頁2行目 |
パラメータ推定結果を入れ，これを引数に加えます |
パラメータ推定結果を入れます |
|
|
|
|
|
第12章
| 221頁図12.2タイトル |
SURモデル |
多変量回帰モデル |
|
| 224頁7-8行目 |
検定統計量は以下の式から |
標準誤差\(s_{12_23}\)は以下の式から |
|
| 226頁13行目 |
総合効果も正で優位 |
総合効果も正で有意 |
|
| 228頁式(12.14) |
＊下記式を参照 |
＊下記式を参照 |
|
| 229頁パス図 |
\(A_{f1},A_{f2}\)の矢印が右向き |
\(A_{f1},A_{f2}\)の矢印が左向き |
|
| 233頁3行目 |
仮定して推定を行うモデルです． |
仮定して推定を行うモデルがあります． |
|
| 234頁6行目 |
Group 1 [0]以下にあるあるのは |
Group 1 [0]以下にあるのは |
|
| 234頁7行目 |
グループの推定家結果です |
グループの推定結果です |
|
| 234頁14行目 |
からAEのパラメータ |
からBEのパラメータ |
|
| 236頁3行目 |
関節効果を検討する |
間接効果を検討する |
|
|
|
|
|
- 228頁式(12.14)
- 誤（0が1列少ない）：
- \[\begin{equation}
\left(\begin{array}{c}
v_1\\
v_2\\
v_3\\
v_4\\
v_5\\
v_6\\
f_1\\
f_2
\end{array}\right) = \mu + \left(\begin{array}{cccccccc}
0&0&0&0&0& \alpha_{17} & \alpha_{18} \\
0&0&0&0&0& \alpha_{27} & \alpha_{28} \\
0&0&0&0&0& \alpha_{37} & \alpha_{38} \\
0&0&0&0&0& \alpha_{47} & \alpha_{18} \\
0&0&0&0&0& \alpha_{57} & \alpha_{28} \\
0&0&0&0&0& \alpha_{67} & \alpha_{38} \\
0&0&0&0&0&0&0 \\
0&0&0&0&0&0&0
\end{array}\right)
\left(\begin{array}{c}
v_1\\
v_2\\
v_3\\
v_4\\
v_5\\
v_6\\
f_1\\
f_2
\end{array}\right) + \left(\begin{array}{c}
\varepsilon \\
\eta
\end{array}\right)
\end{equation}\]
- 正：
- \[\begin{equation}
\left(\begin{array}{c}
v_1\\
v_2\\
v_3\\
v_4\\
v_5\\
v_6\\
f_1\\
f_2
\end{array}\right) = \mu + \left(\begin{array}{cccccccc}
0&0&0&0&0&0& \alpha_{17} & \alpha_{18} \\
0&0&0&0&0&0& \alpha_{27} & \alpha_{28} \\
0&0&0&0&0&0& \alpha_{37} & \alpha_{38} \\
0&0&0&0&0&0& \alpha_{47} & \alpha_{18} \\
0&0&0&0&0&0& \alpha_{57} & \alpha_{28} \\
0&0&0&0&0&0& \alpha_{67} & \alpha_{38} \\
0&0&0&0&0&0&0&0 \\
0&0&0&0&0&0&0&0
\end{array}\right)
\left(\begin{array}{c}
v_1\\
v_2\\
v_3\\
v_4\\
v_5\\
v_6\\
f_1\\
f_2
\end{array}\right) + \left(\begin{array}{c}
\varepsilon \\
\eta
\end{array}\right)
\end{equation}\]
- 補記
- 224頁式(12.10)の標準偏差\(s_{12_23}\)は、\(\alpha_{12}\)と\(\alpha_{23}\)が独立であることを仮定しており、独立ではない場合には不正確になります。間接効果の検証には本文でも述べているブートストラップ法を用いることが一般的です。
第13章
| 241頁式(13.3) |
\(=\frac{p(\theta)p(Data|\theta)}{\int
p(\theta)p(Data|\theta)}\) |
\(=\frac{p(\theta)p(Data|\theta)}{\int
p(\theta)p(Data|\theta)d\theta}\) |
分母に\(d\theta\)を追加 |
|
|
|
|
第15章
| 295頁8,9,10,15行目,296頁2,4行目 |
文中に登場する\(\psi\)はすべて\(\phi\)に修正。 |
|
|
|
|
|
|
謝辞
- ご指摘いただいた皆様、ありがとうございます。
- 大阪大学経済学部2023年度マーケティング２履修者の皆さん
- 五十嵐未来先生（大阪大学）
- 阿部誠先生（東京大学）
- 八木宏瞭さん（阪大院AY2022卒）、井川聖也さん（阪大院）
- 新世社経由でご指摘いただいた皆様
