Rの基礎
1 Rの使い方
本書ではRを使ったマーケティングデータの統計分析を解説しています。そこで、このページでは、Rに初めて触れる方を対象として、インストールと基本的な使い方を補足として説明していきます。すでにRをインストールして使ったことのある方は読み飛ばしていただいても問題ないかもしれませんが、初学者の方向けとして、コンピュータに関する基本的な知識を含めて解説します。
また、このページでは、Rを自分のPCにインストールして使う方法のほかに、ブラウザでRを実行できる環境としてGoogle ColabによるRの使い方についても解説します。Google ColabでRを使う利点もありますので、興味のある方は参考にしてください。
1.1 最速で準備して2章から始めたい方
Google Colabがお勧めです。メニューは以下の通り。
1.1.1 Step 1) 以下のURLをクリックしてRのGoogle Colab notebookを新規作成する。
https://colab.research.google.com/notebook#create=true&language=r
1.1.2 Step 2) データをダウンロードして、Gooogle Colabにアップロードする
2 Rを初めて使う
2.1 インストールして使う
RはThe Comprehensive R Archive Networkからダウンロードし、PCにインストールすることができます。
The Comprehensive R Archive Network (https://cran.r-project.org/)
ウェブサイトにアクセスすると、右上に「Download and Install R」とあり、その下に「Download R for OS名」と表示されていますので、各自使っているOSを選択すればOKです。
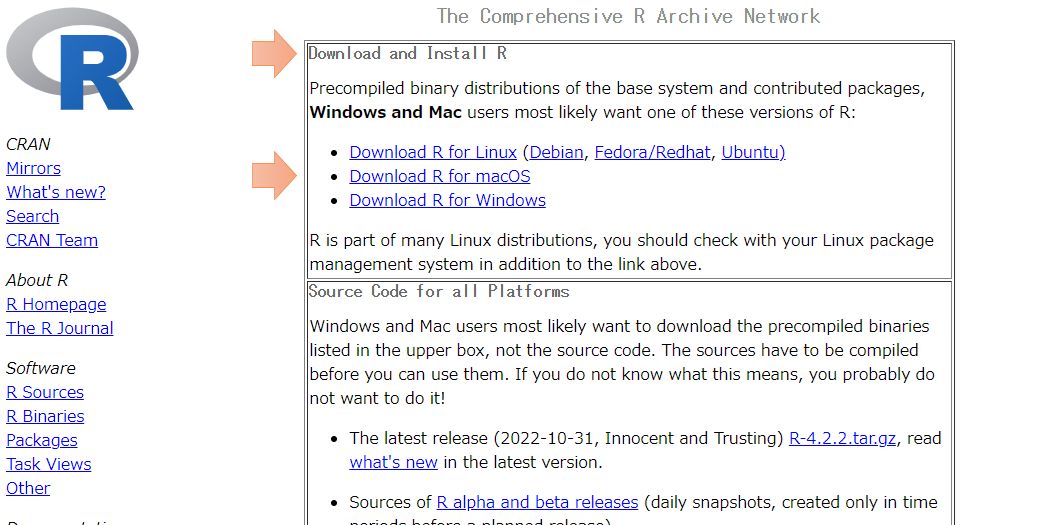
たとえばWindowsのユーザーであれば「Download R for Windows」を選ぶとSubdirectoriesが示されますが、初めてインストールする方は、baseの「install R for the first time」を選んでください。
次の画面の最上部に「Download R ~ for windows(~にはバージョンの数字が入っています)」が出ますので、これをクリックすればファイルがダウンロードされます。あとはダウンロードしたファイルを実行して指示通りにインストールをすれば使えるようになります。
インストールが完了すると、2種類のRが利用可能になります。「R x64 ~」は64bit版のRで、「R i386 ~」は32bit版のRになります。本書で説明している計算であれば、ほとんどどちらを使ってもあまり変わりませんが、取り扱えるデータの最大サイズなどの点で64bit版Rの方が高性能です。本書も基本的には64bit版のRを使っていることを想定して説明していますので、64bit版の方を使ってください。
Rを起動すると以下のような画面が表示されます。ここで、入力を受け付けるのは入れ子になっているウィンドウの「R Console」の部分になります。赤字でカーソルが表示されている部分で入力が受け付けられます。
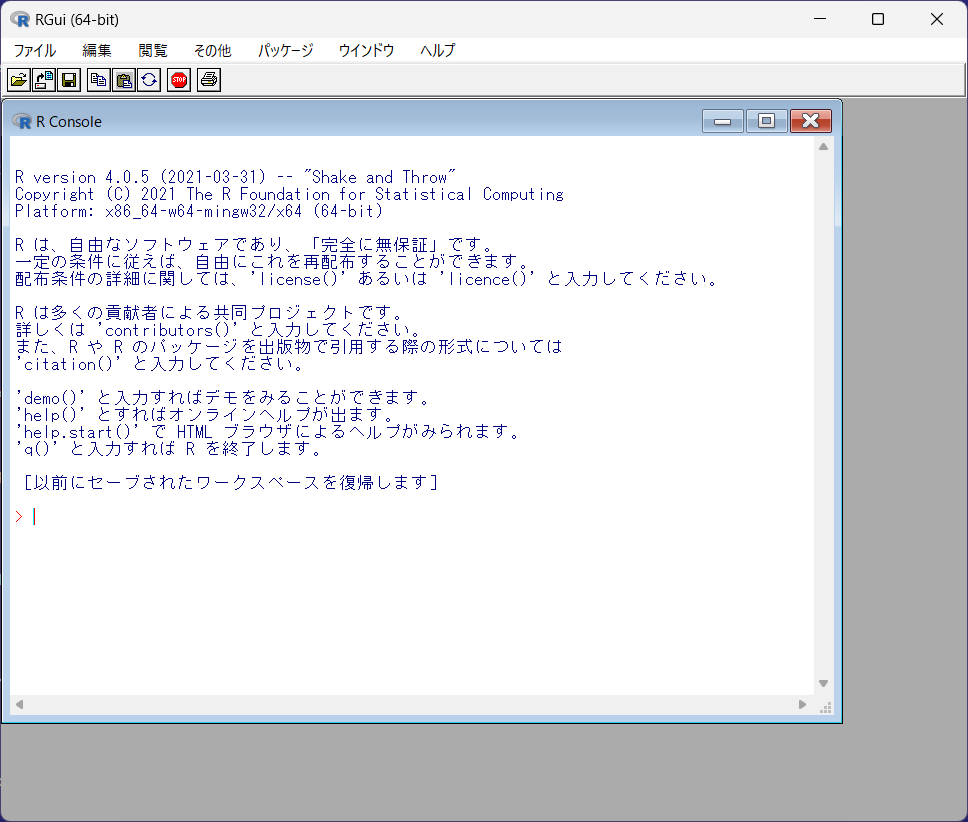
試しに「1+1」と入力してエンターキーを押すと、以下のような結果が出力されます。
1+1## [1] 2\(1+1\)の答えは2になりますので、2が表示されています。
Rではこのようにコマンドを入力してエンターキーを押すことで出力を得ることができます。Rのコンソールに直接書き込むこともできますが、長いコードや複数行にわたる長いコードは別途Rエディタに書き、まとめて実行することができます。Rエディタは「ファイル」→「新しいスクリプト」で作成し、Rファイルとして保存することができます。作成途中のファイルを開くときは「スクリプトを開く」で呼び出すことができます。
ただし、とくに便利な機能がついているわけではないので、実際はRエディタの使い勝手は普通のテキストエディタとあまり変わらないかもしれません。Windowsなら「メモ帳」などに下書きをしてから、コピー+Rにペーストして実行しても構いません。他にも便利なテキストエディタがフリーあるいは安価で入手可能なので、使いやすいものがあればそれを使ってもよいでしょう。
ただし、Microsoft wordなどの「オートコレクト(自動修正)」をするエディタは、大文字小文字を自動修正したり、クオーテーションマークを自動修正したりしてしまい、逆に使い勝手が悪いので注意が必要です。また、テキストエディタで作成したコードを保存しておくフォルダを作っておくとわかりやすいので、予め作業フォルダを作っておきましょう。
基本的なコマンドについてはRの基本的な入出力を参考にして下さい。
また、データのインポート、エクスポートについてはデータのインポート・エクスポートを参考にして下さい。
2.2 RStudioをダウンロードして使う
Rをインストールしてそのまま使うよりも、統合開発環境であるRStudioを使う方が迷うことは少ないかもしれません。レポートの作成やhtmlへの出力もできますので、RStudioをインストールして使うこともお勧めします。
日本語でも多くのインストール方法の解説サイトがありますので、このページでは詳しく解説しませんが、インストールして使うときはこれらのサイトを参考にしてください。
2.3 Google Colabから使う
2.3.1 Google Colab (Google Colaboratory)とは
Rは、基本的にはアプリケーションとして自分のPCにインストールして使ってほしいと考えています。しかしながら、とくにパッケージのインストールで各自のPC環境に関連した解決の難しいエラーに直面することがあります。そこで、どうしても自分の環境でパッケージのインストールができない方は、ブラウザ上でRを実行することができる「Google Colab」を使ってみてください。
Google Colabの利点として、
(P1)ブラウザ上で実行するため各自のPC環境に由来する問題が起こりにくいこと
(P2)複数行のコードを打ち込んでから実行させることができるためエディタが不要であること
(P3)作業ディレクトリの設定を考えなくて良いこと
という利点があり、初めてRを学ぶ方にはよいかもしれません。全員が同じ環境になるので、エラーの解決策も共通のものになります。したがって、教科書通りに実行して、環境に起因するエラーがほとんどないと思われます。また、面倒な作業ディレクトリの指定も不要なので、初学者がRのコマンドだけを学習するとてもよい環境ともいえます。
しかしながら、以下の欠点もあります。
(C1)毎回パッケージをダウンロード&インストールする必要があること
(C2)毎回データをインポートする必要があること
とくに大きなパッケージを複数インストールする必要がある第13章、第14章はGoogle Colabを使うと準備だけで数十分が必要になる可能性もありますので、章によって向き不向きはあります。
いずれにしても、初学者には「簡単に始められる」という利点は大きいですし、原因不明のエラーが起こることも少ないため、本書の前半の章では使う価値も大きいかと思いますので、本節では「Google Colab」でRを実行する手順を説明します。
2.3.2 Google Colabの準備 (1)
最も早い方法は、以下のURLをクリックして新しいGoogle Colab notebookを作ることです。このnotebookはRが使えるようになっていますので、すぐにRを使うことができます。ただし、Google ColabはGoogleが提供しているブラウザサービスなので、まずはGoogleのアカウントを作っておく必要があります。Gmailを使っている場合は、そのまま今持っているGmailのアカウントを使うことができます。
https://colab.research.google.com/notebook#create=true&language=r
開始したnotbookを保存するときは名前を変更して保存してください。
2.3.3 Google Colabの入出力
入力部分は中央部の色の変わった行です。コードを入力して「Ctrl+Enter」を押すか左の再生アイコンをクリックすることでコードを実行することができます。実行結果は直下にすぐ表示されます。3節のコードは全てそのまま実行できるはずです。plotによる図も出力することができます。新しくコードを追加したいときは、「+コード」を押してください。「+テキスト」ではメモを入力する欄を作ることができます。
本書では、各章で新しいデータと分析方法を扱いますので、章ごとに新しいnotebookを作成し、テキストでメモを追記しながら保存しておくことをお勧めします。
2.3.4 Google Colabの準備 (2)
ここからは、Google Colabのnotebookを新規作成する別の方法について解説します。前の節のURLから始めるのが最も早いですが、notebookをアップロードして新しいnotebookを開始することもできます。
アクセスすると以下の画面が出ますので、ログインが必要な場合はGoogleアカウントでログインしてください。
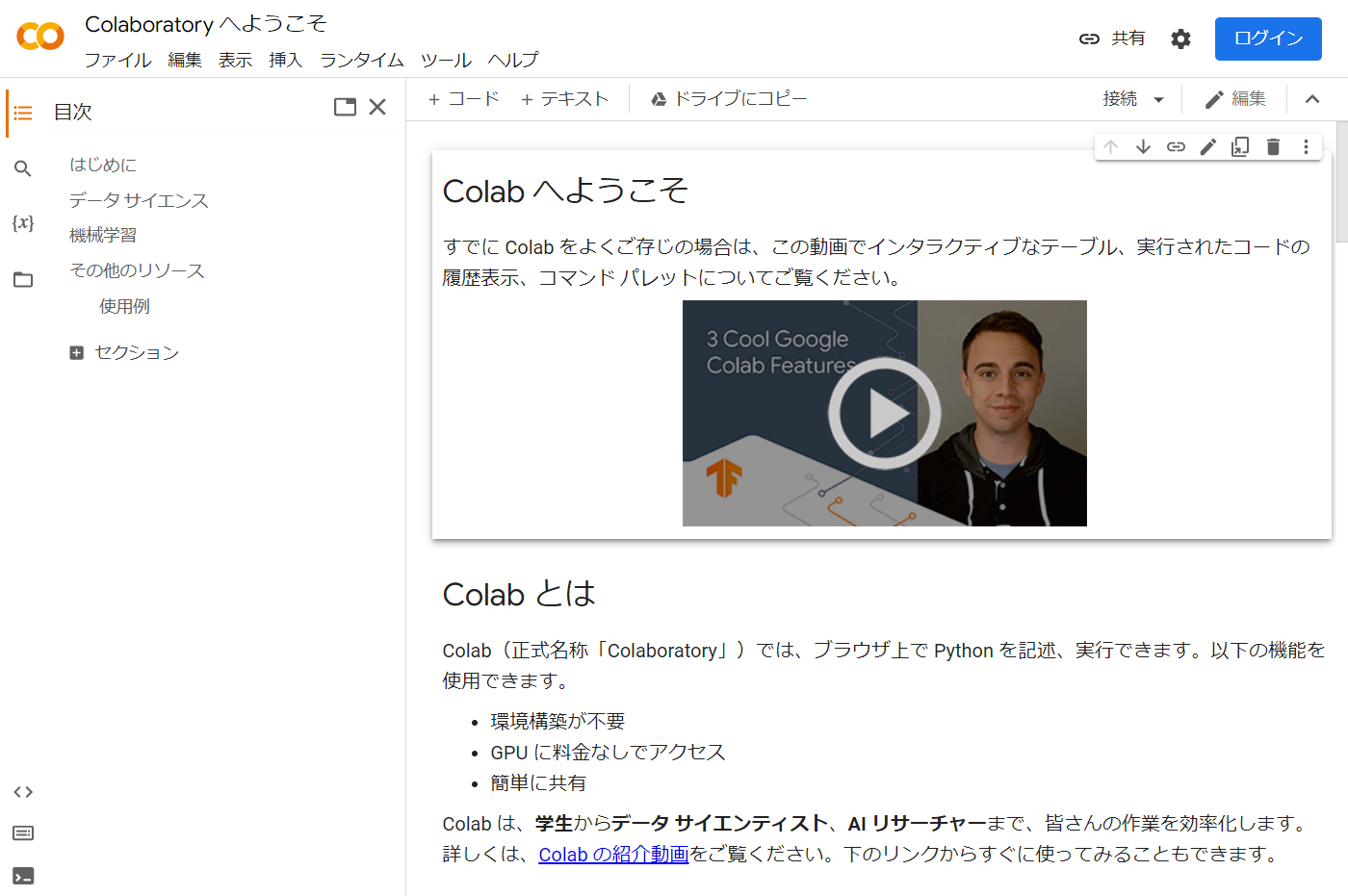
Google Colabの操作はブラウザで行いますが、まずはRが実行できる環境を設定する必要があります。デフォルトではpython 3の実行環境になっているので、この部分だけ変えてRの実行環境にしましょう。
まず、「Colaboratoryへようこそ」の画面で左上「ファイル」を選び、「ノートブックを新規作成」を選びます。ここで新しい画面が開きますが、この画面ではまだRを使うことはできません。
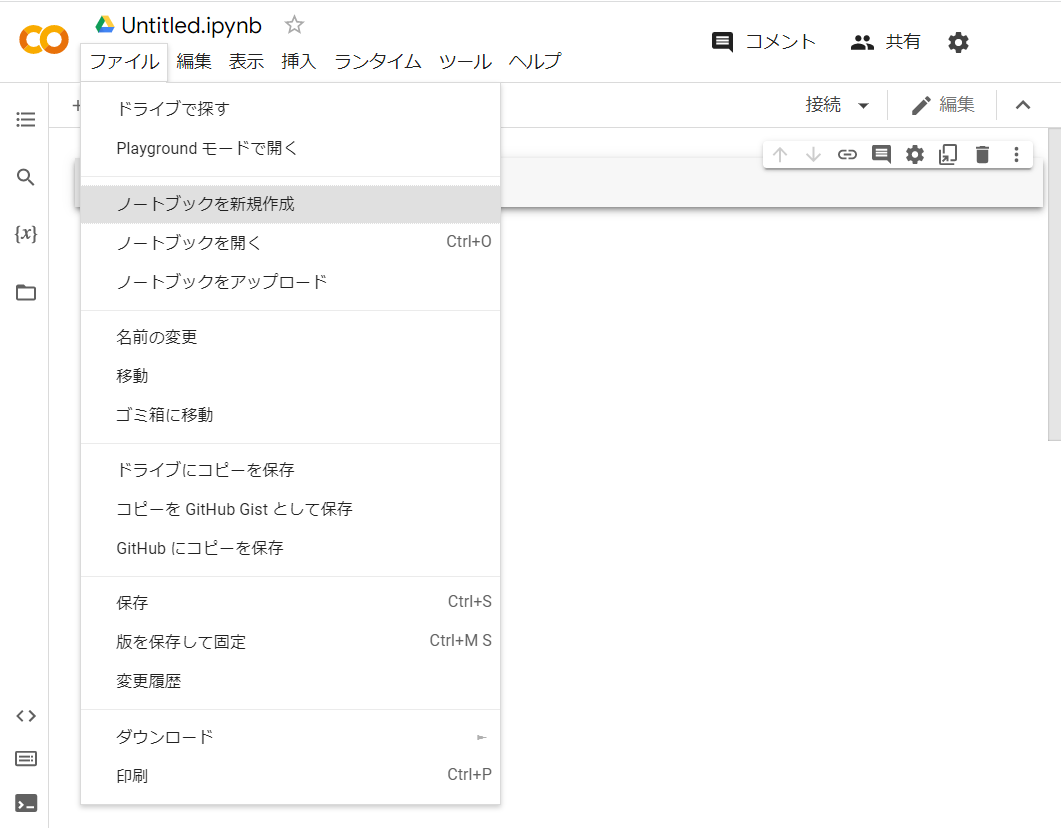
次に、この画面でまた左上の「ファイル」を選び、下の方にある「.ipynbのダウンロード」でファイルをダウンロードします。おそらく「Untitled.ipynb」などという名前がついていると思います。このファイルをノートパッドなどで開くと、10行目と11行目には以下のようなコードが書かれています。
10 | "name" : "python3",
11 | "display_name" : "Python 3",これは実行環境がpython 3になっているということなので、Rに修正します。
10 | "name" : "ir",
11 | "display_name" : "R",これで名前を「R_Colab.ipynb」などに変更して保存しておきます。新しくGoogle ColabでRを使いたいと思ったときは、毎回このファイルを使うことができます。
参考までに、R_Colab.ipynbを置いておきますので、上記の修正がうまくいかない方は↓のzipファイルをダウンロードし、解凍して使ってください。
ファイルができたら、また「Google Colabへようこそ」の画面に戻り、「ファイル」→「ノートブックをアップロード」を選びます。ここでファイルをドラッグ&ドロップできる画面が表示されますので、「R_Colab.ipynb」をアップロードしてください。これでRを使える環境が整いました。
3 Rの基本的な入出力
3.1 コマンドの入力
「1+1」と入力してエンターキーを押すと、以下のような結果が出力されます。
1+1## [1] 2\(1+1\)の答えは2になりますので、2が表示されています。その前に表示されている「[1]」は、表示される答えの「ベクトル上での位置」になります。Rでは、数値を行列やベクトルとして解釈しています。1+1の答えはスカラーですが、1次元のベクトルとして認識し、その第1要素が2という答えを表示していることになります。多次元のベクトルや行列を扱うときにはこの要素の位置が参考になることもありますが、ここではあまり気にしなくても大丈夫です。
3.2 四則演算とオブジェクト
3.2.1 基本的な計算
基本的な計算(四則演算)には以下のコードを使います。
- 加算(\(1+1\))、\(2\)が出力されます。
1 + 1 ## [1] 2- 乗算(\(2×2\))、\(4\)が出力されます。
2 * 2 ## [1] 4- 減算(\(3-4\))、\(-1\)が出力されます。
3 - 4 ## [1] -1- 除算(\(6/2\))、\(3\)が出力されます。
6 / 2 ## [1] 33.2.2 オブジェクトを使った計算
何度も参照、計算する場合、文字を1つ定義して、その文字に入っている値で計算を行うこともできます。この文字のことを「オブジェクト」といいます。
x <- 1 # オブジェクトxに1を代入する。
y <- 3 # オブジェクトyに3を代入する。
x + y # x + yなので4が出力される。## [1] 4X <- 4 # Xに4を代入。大文字と小文字は異なるものとして識別されるので注意。
X + y # X + yなので7が出力される。## [1] 7オブジェクトを定義したときや値を代入したとき、Rからは何のメッセージも出ませんが、とくにエラーメッセージが出なければ成功しています。Rにはオブジェクトが記録されていますので、自分が定義したオブジェクトを確認することができます。
ls() # 作業スペースにあるオブジェクトを見る。## [1] "x" "X" "y"rm(x,y) # オブジェクトx,yを削除する。
ls() # もう一度作業スペースにあるオブジェクトを見る。## [1] "X"また、先ほどのスカラーとベクトルの話でもありましたが、ベクトルとしてオブジェクトを定義することもできます。以下はどちらも同じベクトルを定義するコードです。コードの書き方は1通りではありませんので、書きやすい表現で書いてもらえれば大丈夫です。
# x =(1,⋯,10)とするコード1。
x <- 1:10
x## [1] 1 2 3 4 5 6 7 8 9 10# x =(1,⋯,10)とするコード2。
x <- c(1,2,3,4,5,6,7,8,9,10)
x## [1] 1 2 3 4 5 6 7 8 9 103.3 集計と変換の関数
データは多くの場合ベクトルとして得られています。Rでは集計と変換の関数によって簡単にデータの集計値を得ることができます。まず、以下のような100次元のベクトルxを定義して、これを集計・変換する基本的な関数を紹介していきます。
- \(x = (1,\cdots,100)\)を定義する。
x <- 1:100 #基本的な集計関数は以下の通りです。
# 集計情報として、最小値(Min.), 第1四分位点(1st Qu.), 中央値(Median)、平均値(Mean)、第3四分位点(3rd Qu.)、最大値(Max)を出力する。
summary(x)
# 総和を出力する。
sum(x)
# 算術平均値を出力する。
mean(x)
# 中央値を出力する。
median(x)
# 分散(不偏分散)を出力する。
var(x)
# 標準偏差を出力する。
sd(x)
# 総積を出力する。
prod(x)次に示す変換の関数については、すべてベクトルの要素ごとに一回で計算されます。
# xの平方根を出力する。
sqrt(x)
# xの自然対数を出力する。
log(x)
# 2つめの引数に10(底)を指定してxの常用対数を出力する。
log(x,10)
# xの指数e^xを出力する。
exp(x)
# 小数点以下切り捨て。
floor(x/10)
# 小数点以下切り上げ。
ceiling(x/10)
# 小数点以下四捨五入。
round(x/10)
# 剰余演算子。x÷10の余りを要素ごとに出力する。
x%%10 help(round) # 関数の詳細についてはhelpを参照できる(この例では関数roundの詳細)。3.4 データの型
Rではデータを格納するときに型が定義されます。基本的には演算ができるのは数値(numeric)型と一部論理(logical)型になります。たとえば数字が入っていても、それが文字列(character)型として認識されていた場合、計算ができないというエラーが返ってきます。関数modeで変数の型を確認することができます。
numeric(数値)型:四則演算ができる一般的な実数値です。以下、c(1,2,3,4,5)はベクトルの定義です。cで数値を囲うとベクトルとして定義できます。
x1 <- c(1,2,3,4,5)
mode(x1) ## [1] "numeric"logical(論理)型:TRUE(1)およびFALSE(0)の2値をとる論理(ブール)型変数です。FALSE=0と,TRUE=1として計算することも可能です。
x2 <- (x1 < 3)
mode(x2)## [1] "logical"sum(x2) ## [1] 2logical型は比較演算子「==」の戻り値でもあります。ここで、「!=」は等しくないという意味「!」は否定演算子です。
2 == 3## [1] FALSE2 != 3 ## [1] TRUEcharacter(文字列)型:文字として認識するため、数字が入っていても演算はできません。
x3 <- c("A", "B", "C")
mode(x3) ## [1] "character"x4 <- c("1", "2", "3")
mode(x4)## [1] "character"型変換には「as.xx」を使います。この例では文字列型で数値が入っていたx4を数値型に変換し、オブジェクトx5としています。
x5 <- as.numeric(x4)
mode(x5) ## [1] "numeric"また、少し特殊な型で因子型(カテゴリー型)、順序付き因子型のデータとして持つこともできます。この場合、因子型なので演算は少し制限が掛かりますが、名義尺度の情報を管理するときに便利です。とくに、集計(table関数)を使うときにはオプションlevelsを活用しましょう。
要素が1,2,3,5のいずれかになるようなオブジェクトx0を定義します。
x0 <- c(1,1,2,2,2,3,3,3,3,5) 因子型への変換 - x1: 関数factorで因子型に変換できます。 - x2: 関数orderedで順序付き因子型に変換できます。 - x3: xの要素では1,2,3,5が観測されていますが、実際は1,2,3,4,5の値を取りうるデータのとき、(例えば5段階評価など)levelsというオプションで指定することができます。
x1 <- factor(x0)
x2 <- ordered(x0)
x3 <- factor(x0,levels=1:5)levelsを指定したとき(x3)と指定しないとき(x1)ではtable関数での集計結果が異なります。
table(x1)## x1
## 1 2 3 5
## 2 3 4 1table(x3) ## x3
## 1 2 3 4 5
## 2 3 4 0 13.5 特殊なデータ
数値を0除算するときにはInf、文字列型を強制的に変換するときにNAという特殊な文字が生成されることがあります。他にもNULLやNaNなどがありますが、こうしたデータの不在や欠損に関する情報が入っていた場合、少し特殊な処理が必要になります。
# 文字列を数値に変換: NAが出力される。
as.numeric("A")## Warning: 強制変換により NA が生成されました## [1] NA# 0除算: Infが出力される。
10/0## [1] Inf# 0/0: NaNが出力される。
0/0## [1] NaN# NULLはデータのサイズも何も情報がないことを示す。
x1 <- NULL
# 値がNULLであるか判定する関数is.null
is.null(x1)## [1] TRUE# NAはデータのサイズはあるが、欠損していることを示す。
x3 <- NA
# 値がNAであるか判定する関数is.na
is.na(x3)## [1] TRUE# Infは∞、-Infは-∞を示す。
x4 <- Inf
# 値がInfあるいは-Infであるか判定する関数is.infinite
is.infinite(x4)## [1] TRUE特殊なデータが含まれていると、そのまま集計関数などを使うことができません。
x0 <- c(1,2,NA,3,NA,4,5)
sum(x0)## [1] NANAを含むデータを集計する場合、na.rmというオプションがある集計関数もあります。または関数is.naでNAを検知して除外するなどの処理が必要です。
sum(x0,na.rm=TRUE)## [1] 15sum(x0[!is.na(x0)])## [1] 153.6 データの構造
Rでは変数をベクトルだけでなく、行列、配列、リスト、データフレームなどの構造でもつことができます。
# v1,v2はともに5次元のベクトルである。
v1 <- c(1,2,3,4,5)
v2 <- 6:10
is.vector(v1)## [1] TRUEis.vector(v2)## [1] TRUE# v3はv1とv2を列(column)に格納した5×2の行列。
v3 <- cbind(v1,v2)
is.matrix(v3)## [1] TRUE# v4はv1とv2を行(row)に格納した2×5の行列。
v4 <- rbind(v1,v2)
is.matrix(v4)## [1] TRUE# v5は2×2の行列。
v5 <- matrix(0,2,2)
# v6は2×2×2の配列(アレイ)。
v6 <- array(0,dim=c(2,2,2))
# v6は配列であり行列ではないが、v5は配列でも行列でもある。
is.array(v6)## [1] TRUEとくに、リスト、データフレームは特殊な構造なので注意が必要ですが、自由度も高いので性質を知ればRのプログラムが簡単になります。
- リスト
# リストは異なる構造のデータを1つにまとめたオブジェクト
list1 <- as.list(NULL)
# リスト[[1]]に3次元ベクトルを代入。
list1[[1]] <- 1:3
# リスト[[2]]には4次元ベクトルを代入。異なるサイズのオブジェクトと1つのオブジェクトにまとめることができる。
list1[[2]] <- 4:7
# リストの呼び出しは[[・]]を使い、さらに[・]から要素を呼び出すことができる。
list1[[2]][2]## [1] 5- データフレーム
# データフレーム:一見行列型であるが、列ごとに型が異なっていてもよい
data1 <- data.frame(x=1:3,y=c(F,F,T))
# データフレームは行列ではないので、行列演算ができないので注意。
is.data.frame(data1)## [1] TRUEis.matrix(data1) ## [1] FALSE3.7 乱数の発生と反復処理
Rには乱数(疑似乱数)を発生させる関数が実装されています。実は乱数は多方面で利用されており、シミュレーションや数値計算などを通じて、実生活に役立つ多くの知識が乱数によってもたらされています。乱数は1回発生させただけではあまり使えませんが、1000回や10000回など、数多くの試行を繰り返すことによって近似値の計算を行うことができます。そこで本節では合わせて反復処理(ループ)についても説明します。
# 乱数のシード値を設定する。()内の数字が同じなら常に同じ乱数を発生させる。
set.seed(1)乱数を発生させて円周率の近似値を求めることもできます。
# 発生させる乱数の数を決める。
n <- 1000
# x, y座標を表す2組の一様乱数を生成する。
x <- runif(n)
y <- runif(n)
# (x,y)平面上で、 x^2+y^2<1なら真(1)、そうでなければ偽(0)を取る変数qを作成する。
q <- (x^2 + y^2) < 1
# その点を平面にプロットする。円の外側と内側で0,1がわかれている。
plot(x,y,pch=q+1)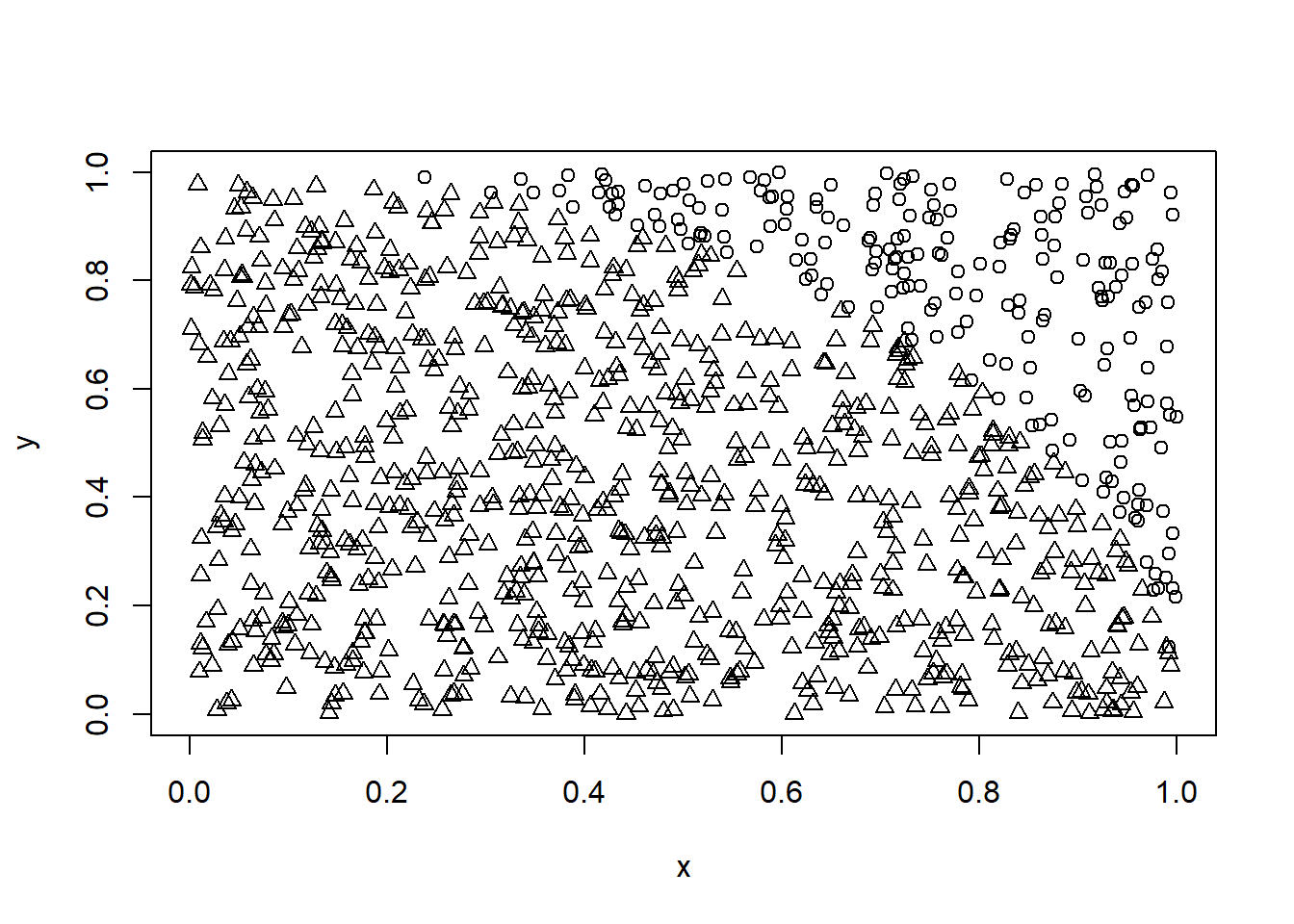
以下の値を計算すると、円周率の近似値を得ることができます。
\[ \hat{\pi} = 4 \times \frac{1}{n}\sum_{i=1}^{n} q_i \]
4*(1/n)*sum(q)## [1] 3.148発生させる乱数の数nを増やしていけば精度も向上していきます。以下のコードでは、反復処理を使って繰り返し回数を10(1e+01)回、100(1e+02)回、1000(1e+03)回、・・・、1千万(1e+07)回まで増やしたときの円周率の近似値を計算します。
# 発生させる乱数の数をベクトルで定義する。
n <- 10^(1:7)
n## [1] 1e+01 1e+02 1e+03 1e+04 1e+05 1e+06 1e+07# pihatという7次元の0ベクトルを定義する。
pihat <- numeric(7) 以下がループ(反復処理)になります。ループ内で、\(x^2+y^2<1\)なら真(1)、そうでなければ偽(0)を取る変数を作成し、pihatの第i要素に計算結果を代入します。
for(i in 1:7){
x <- runif(n[i])
y <- runif(n[i])
q <- (x^2 + y^2) < 1
pihat[i] <- 4*(1/n[i])*sum(q)
}反復処理の基本構造は以下のようになっています
for (インデックス in 1:繰り返し回数){
反復する処理
}最後に、計算結果を表に出力してみます。
plot(n,pihat,log="x",type="b")
abline(pi,0) 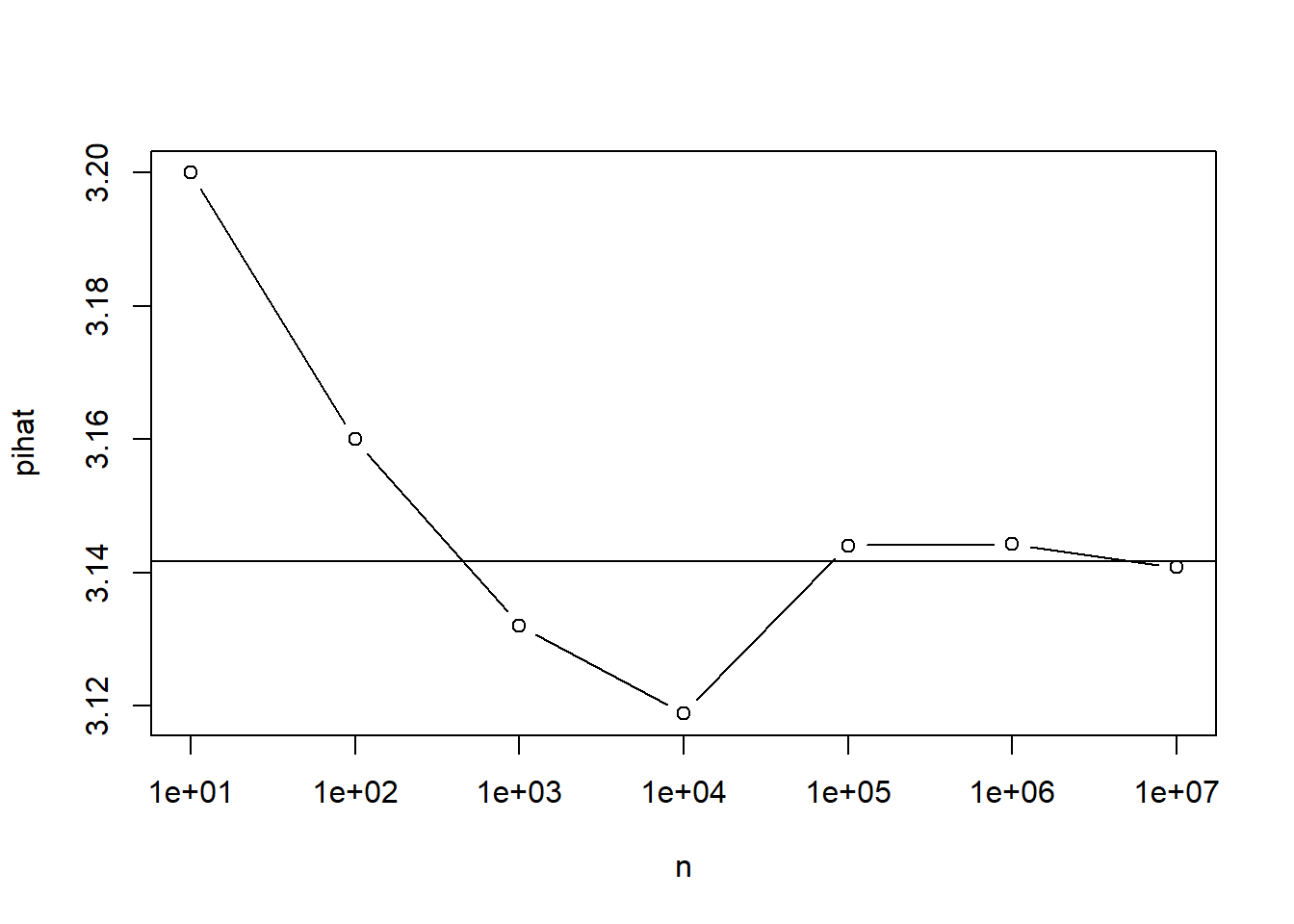
3.8 行列の演算
3.8.1 行列の定義
データは行列かベクトルとして扱われますが、行列であれば行列演算を行うことができます。ただし、行列演算ができるのはmatrix型のオブジェクトだけです。3.4節で説明した、一見行列なのに行列ではないdata.frame型では行列演算ができないので、関数as.matrixによって変換させる必要があります。
# 行列a,bを定義する。aは2×2の行列、bは2×1の行列、cは2×2の単位行列である。
a <- matrix(1:4,2,2)
b <- matrix(1:2,2,1)
# cは2×2の単位行列である。
c <- diag(2)一般的な行列の定義は、matrix(要素, 行数, 列数)で、要素とサイズを指定します。また、単位行列を出力する関数diagなど、いくつか特殊な行列を作る関数があります。
また、行列を要素ごとに定義することもできます。四則演算とオブジェクトで、関数cでベクトル定義する方法を紹介していますが、定義したベクトルさらに束ねることで行列を定義することができます。ベクトルを行(row)で束ねるときは関数rbind、列(column)で束ねるときは関数cbindを使います。
# 行列Aを定義する。cで定義したベクトルを関数rbindで行に束ねる。
A <- rbind(
c(4,3,2,1),
c(3,2,0,1),
c(0,0,3,0),
c(0,1,0,3))
A## [,1] [,2] [,3] [,4]
## [1,] 4 3 2 1
## [2,] 3 2 0 1
## [3,] 0 0 3 0
## [4,] 0 1 0 3# 行列Bを定義する。関数cbindで列にまとめる。
B <- cbind(
c(4,3,2,1),
c(3,2,0,1),
c(0,0,3,0),
c(0,1,0,3))
# Aの転置とBが同じ行列になる。
B## [,1] [,2] [,3] [,4]
## [1,] 4 3 0 0
## [2,] 3 2 0 1
## [3,] 2 0 3 0
## [4,] 1 1 0 3t(A)## [,1] [,2] [,3] [,4]
## [1,] 4 3 0 0
## [2,] 3 2 0 1
## [3,] 2 0 3 0
## [4,] 1 1 0 3なお、行列は配列かという判定にはTRUEが返りますが、データフレームでありません。
is.matrix(a)## [1] TRUEis.array(a)## [1] TRUEis.data.frame(a)## [1] FALSE3.8.2 要素ごとの計算
行列で四則演算子などをそのまま使うと要素ごとの計算になります。後述する行列積などとは答えが変わってくるので注意してください。
a + c## [,1] [,2]
## [1,] 2 3
## [2,] 2 5a - c## [,1] [,2]
## [1,] 0 3
## [2,] 2 3a * c## [,1] [,2]
## [1,] 1 0
## [2,] 0 4c / a## [,1] [,2]
## [1,] 1 0.00
## [2,] 0 0.25四則演算子は要素ごとの計算なので、基本的には行列のサイズが違うと計算はできませんが、例外として、サイズ1x1の行列または1次元ベクトルはスカラー扱いになるため、計算することができます。
a[2,2]## [1] 4a[2,2] * b## [,1]
## [1,] 4
## [2,] 8a[2,2] - c## [,1] [,2]
## [1,] 3 4
## [2,] 4 33.8.3 行列計算
行列積やクロネッカー積(\(\otimes\))の計算などには演算子または関数が用意されています。
# 行列積の計算には「%*%」を使う。
a %*% c## [,1] [,2]
## [1,] 1 3
## [2,] 2 4a %*% b## [,1]
## [1,] 7
## [2,] 10# 行列の転置にはt(・)を使う。
t(b) %*% a## [,1] [,2]
## [1,] 5 11# クロネッカー積の計算には「%x%」または関数kroneckerを使う
b %x% a## [,1] [,2]
## [1,] 1 3
## [2,] 2 4
## [3,] 2 6
## [4,] 4 8kronecker(b,a)## [,1] [,2]
## [1,] 1 3
## [2,] 2 4
## [3,] 2 6
## [4,] 4 8また、逆行列や固有値・固有ベクトルを計算することもできます。
# 関数solveで逆行列が計算できる。
solve(a)## [,1] [,2]
## [1,] -2 1.5
## [2,] 1 -0.5# 関数eigen固有値分解を行う。$valuesで固有値、$vectorsで固有ベクトルを得ることができる。
ae <- eigen(a)
ae$values## [1] 5.3722813 -0.3722813ae$vectors## [,1] [,2]
## [1,] -0.5657675 -0.9093767
## [2,] -0.8245648 0.4159736コレスキー分解を行う関数も用意されています。関数cholの引数に行列\(X\)をとると、行列\(X\)から、\(X=L' L\)となる上三角行列\(L\)を得ることができます。
d <- 2*c+1
d## [,1] [,2]
## [1,] 3 1
## [2,] 1 3ld <- chol(d)
ld## [,1] [,2]
## [1,] 1.732051 0.5773503
## [2,] 0.000000 1.6329932t(ld)%*%(ld)## [,1] [,2]
## [1,] 3 1
## [2,] 1 34 データのインポート・エクスポート
本書では、Rを使って様々なデータを分析していきますが、分析の前にはデータを読み込ませる必要があります。具体的には別に用意されたデータファイルをRに読み込まるのですが、これを「インポート」といいます。普段PC使ってレポートを作成するときなどは、ファイルを開いて文字や図表を加えて保存する、という作業すると思いますが、このような、ファイルを直接開く方法と異なる点が1つあります。Rではファイルからデータをインポートしますが、Rの中であるファイルからインポートしたデータを変更させても元のファイルは変更されません。Rのインポートは、元のファイルのデータをコピーしてRの中に分析ができる形のデータとして新しくオブジェクトを作る、という作業になりますので注意が必要です。Rの中で変更させたデータをファイルに書き出すこともできますが、この作業は「エクスポート」といいます。
まずは以下のファイルをダウンロードしてください。このファイルのように、データはcsv (comma-separated values; カンマ区切り数値)ファイルやtsv (tab-separated values; タブ区切り数値)ファイルとしてまとめられており、集計・分析するためにはRにインポートしなければなりません。
以降では、まずは「Rをインストールした場合」のインポート方法について説明します。Google Colabを使う場合はGoogle Colabを使う場合を参照してください。
4.1 Rをインストールした場合
RをPCにインストールした場合、データをRに読み込ませる(インポートする)ためには、ファイルの正確な名前と作業ディレクトリ(ワーキングディレクトリ)を把握しなければなりません。そこで、まずは拡張子の表示、ワーキングディレクトリの確認について説明しなければなりません。そこで、本節ではまずは拡張子の表示方法とディレクトリ構造の説明をします。すでに知っているという方は飛ばしてしまって構いません。
4.1.1 ファイルの拡張子を表示する
Rにデータをインポートするためには、ファイル名を指定してデータを読み込ませる必要がありますが、多くのPCではファイルの正確な名前は表示されていません。ファイル名には一般に「拡張子」という情報が付されており、この拡張子を含めた名前がファイルの正式な名称になります。具体的には、「filename」としてテキストエディタで開くことのできる文書は「filename.csv」となっており、「.csv」の部分が拡張子になります。インポートするファイル名を指定するときは、この拡張子込みのファイル名を入力する必要があります。
拡張子の表示のさせ方はOSによって違いますが、Windowsであれば、フォルダを開いて「表示」タブを開き、「表示/非表示」欄の「ファイル名拡張子」にチェックを入れることでファイルを拡張子込みで表示させることができます。また、あわせて「隠しファイル」もチェックしておくとよいかもしれません。Mac OCの場合は、「Finder」→「環境設定」→「詳細」を選択し「すべてのファイル名拡張子を表示」を選択すると拡張子が表示されます。
4.1.2 絶対パス、相対パス
拡張子を含めたファイル名が表示されたら、次にデータファイルの位置を指定してインポートする必要があります。現在我々が使っている多くのOSでは、階層型(ツリー型)ファイルシステムといって、すべてのファイルが階層的に配置されています。簡単にいうと、我々が使っている住所と同じ表現でファイルの位置を特定することができる仕組みになっています。たとえば住所でいえば
「日本/大阪府/豊中市/待兼山町/1/7」
のように国名、都道府県名、市町村名、といった階層ごとに区切りながら表現していくことで全ての住所を表現することができます。PC内の住所も同様です。ディレクトリ(フォルダともいいます)が入れ子になっていて階層的にファイル名の場所を指定するのです。WindowsとMac OS (Unix)で1箇所だけ違うのは、最上位(大元)がドライブ名かルートディレクトリかの違いで、Windowsでは「C:」などのドライブ名、Mac OSなら「/」だけのルートディレクトリが最上位になります。ここから、たとえばディレクトリ「d11」→ディレクトリ「d21」→ディレクトリ「d32」にある「dat1.txt」というファイルを指定したいときには、Windowsなら
「C:/d11/d21/d32/dat1.txt」
となりますし、Mac OSなら
「/d11/d21/d32/dat1.txt」
となります。これをファイルパスとよび、「/」は区切り記号といい、階層を分ける役割があります。このようにルート(ドライブ)から全てのディレクトリを明示する指定方法を「絶対パス」によるファイル指定といいます。なお、Rの区切り記号は「¥¥」(¥¥を2回、環境によってはバックスラッシュ「\」が表示されることもありますが、Windowsでは区別しません)や「/」を使うことができます。ただし、Mac OSでは「¥」と「\」を区別するので、「/」を使わないのであれば「¥」の代わりにoptionキーを押しながら「¥」キーを押すと出るバックスラッシュ「\」を使う必要があります。
また、パスの指定方法はもう1つあり、Rが作業をしている「ワーキングディレクトリ(WD)」からの相対的な位置で指定する方法です。このためには、まずRのWDがどこなのか知っておく必要があります。Rが作業しているディレクトリは関数getwdで取得することができます。たとえばWDが
「C:/d11/d21/d32」
だったとき、「d32」というドライブで作業していることになりますので、「d32」にある「dat1.txt」を呼び出すときには「dat1.txt」だけを指定すれば呼び出すことができます。相対パスでは、パスが短くなるという利点があります。作業ディレクトリの変更には、コマンドでは関数setwdを使いますが、次の節で説明するように、「ファイル」から変更することもできます。
4.1.3 簡単な初期設定方法
ここからの作業は「ディレクトリ構造がよくわからないので自分で作業ディレクトリの設定できない」という方向けなので、自分で設定できるという方は作業がしやすいディレクトリを自分で作ってください。
まず、デスクトップ上で右クリックし「新規作成」→「フォルダ」で新しいフォルダを作ります。フォルダには「Rfiles」という名前を付けてください。
続いて、Rを起動し、「ファイル」→「ディレクトリの変更」で「デスクトップ」の「Rfiles」を選択して「OK」を押します。これで作業ディレクトリを変更させることができました。コンソールにgetwd()と入力して戻り値を確認すると、Windowsなら
「(ドライブ名):/Users/(ユーザー名)/Desktop/Rfiles」
Mac OSであれば
「/Users/(ユーザー名)/Desktop/Rfiles」
になっているはずです。このように表示されていれば作業ディレクトリがデスクトップ上のフォルダRfileに設定されている状態です。
引き続きRから「ファイル」→「作業スペースの保存」を選びます。ここで確認が出ますので、そのまま「保存(S)」をしてください。ここで、デスクトップ上に作られたディレクトリ「Rfiles」の中に新しいファイル「.RData」が追加されているはずです。インポートしたいデータをディレクトリ「Rfiles」にそのまま入れれば、相対パスでファイル名だけを指定すればインポートできることになります。これからいろいろな課題でRを使いますが、毎回作業ディレクトリの設定を行うのが面倒なら、Rfilesにある「.Rdata」から起動することもできます。
ここまで準備できた方はデータのインポートと操作に進んでください。
4.2 Google Colabを使う場合
インポートしたいデータがあるときはファイルをアップロードすることができます。左列のフォルダアイコンをクリックすると「ファイル」の一覧を見ることができます。この欄にインポートしたいファイルを直接ドラッグ&ドロップすることができます。アップロードされた時点ではまだインポートはされていないので注意してください。また、ファイルはずっと保存されているわけではないので、毎回アップロードする必要があります。自分のPCに保存しているデータファイルも削除しないようにしてください。
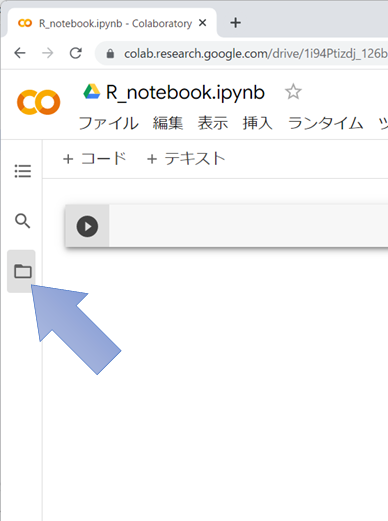
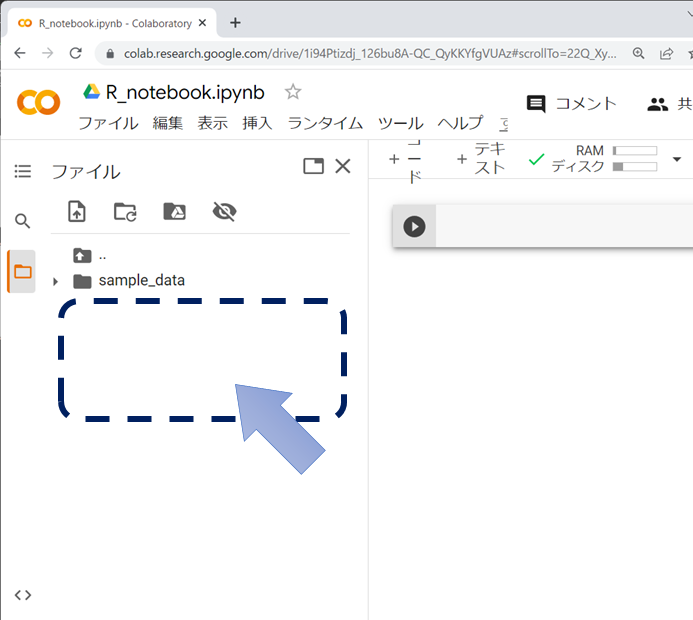
アップロードされたデータとコード入力の作業スペースは同じディレクトリにあることになっていますので、とくにパスを指定せず、ファイル名だけを指定してインポートすることができます。ファイルをアップロードしただけではデータの分析はできず、インポートする必要がある点に注意してください。また、エクスポートしたファイルも同じように出力されますので、ダウンロードして保存してください。
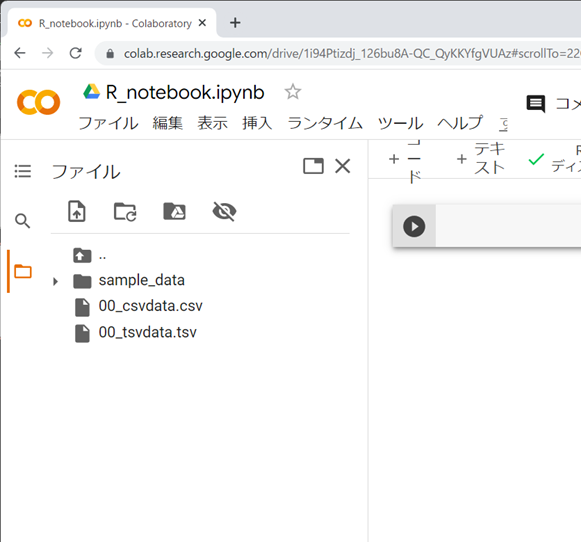
ファイルをアップロードできれば、以降のコードはそのままGoogle Colabでも使うことができます。
4.3 データのインポートと操作
4.3.1 データをインポートする
では、データをインポートしてみましょう。まずはインポートするデータファイルを作業ディレクトリにダウンロードします。またはデータを保存しているディレクトリへ作業ディレクトリを変更します。
2つのファイル「00_csvdata.csv」と「00_tsvdata.tsv」はどちらもエクセルやテキストエディタで開くことができると思いますが、データの数値自体は同じものです。違うところは区切り記号です。それぞれインポートする際に区切り記号を指定する必要があります。
# csvならread.csvでインポートができる。
# データの1行目がheaderならheader =TRUEとする。
x11 <- read.csv(file = "00_csvdata.csv", header = TRUE)
# read.tableでセパレータ(sep)を指定することもできる。
# csvならsep=","と指定する。
x12 <- read.table(file = "00_csvdata.csv", sep=",", header = TRUE)
# tsvはタブ区切りなのでsep="\t"とする。
# MacOSならoption+\でバックスラッシュを指定する。
x22 <- read.table(file = "00_tsvdata.tsv", sep="\t", header = TRUE)なお、無事インポートできたら何もメッセージは出ませんが、オブジェクト名をコマンドで入力するとデータの中身を見ることができますので確認してください。インポートされていたらデータがきれいに表示されるはずです。
4.3.2 インポートしたデータの操作
インポートができたらデータを少し操作してみましょう。
# オブジェクトxにx11のデータをコピーする。
x <- x11
#オブジェクトがdata.frame型であるか確認する。
is.data.frame(x)## [1] TRUE#データの要約を出力する。
summary(x)## id x y
## Min. : 1.00 Min. :0.04113 Min. :0.1894
## 1st Qu.: 3.25 1st Qu.:0.31407 1st Qu.:0.3494
## Median : 5.50 Median :0.56181 Median :0.5010
## Mean : 5.50 Mean :0.53459 Mean :0.5121
## 3rd Qu.: 7.75 3rd Qu.:0.82798 3rd Qu.:0.5666
## Max. :10.00 Max. :0.91691 Max. :0.9252データの一部を抜き出すには以下のような命令を使います。
#[,1]でデータの1列目を抜き出して表示する。
x[,1]## [1] 1 2 3 4 5 6 7 8 9 10#idという名前の列を抜き出して表示する。
x$id## [1] 1 2 3 4 5 6 7 8 9 10#データの1行1列目を抜き出して表示する。
x[1,1]## [1] 1#データの1行1列目~2行2列目を抜き出して表示する。
x[1:2,1:2]| id | x |
|---|---|
| 1 | 0.5190332 |
| 2 | 0.8747620 |
また、インポートしたデータはデータフレーム型(data.frame)になっているので、行列計算をする場合には関数as.matrixで型の変換をする必要があります。
# xをmatrix型に変換したオブジェクトxmを定義する。
xm <- as.matrix(x)
#共分散行列を出力する。
var(xm[,2:3])## x y
## x 0.09919008 0.03076054
## y 0.03076054 0.05221904#相関係数を出力する。
cor(xm[,2:3])## x y
## x 1.0000000 0.4274107
## y 0.4274107 1.0000000#行列演算をする。
t(xm[,2:3])%*%xm[,2:3]## x y
## x 3.750600 3.014386
## y 3.014386 3.092232# xmの2列目と3列目の和zを定義する。
z <- xm[,2]+xm[,3]
# 「xm」と「z」を束ねた行列xoを定義する。
xo <- cbind(xm,z)4.3.3 データをファイルにエクスポートする
最後に上記のオブジェクトxoをエクスポートします。fileでファイル名をoutdata.txtと指定し、区切り記号はタブとしています。また、デフォルトでは行番号が入るところをrow.names=FALSEで行番号を出力しない設定にしています。
# エクスポートのコマンドはwrite.table
write.table(xo, file = "outdata.txt", sep = "\t", row.names = FALSE)
# dir()でディレクトリの中のファイルを確認できる。
# outdata.txtがあればファイルのエクスポートは成功。
dir()