S4 オンライン付録

このページでは，紙幅の都合で省略した補足説明を掲載している．本文との対応関係は以下のとおりである．

章	本文頁数	参照箇所
第1章	41頁	S4.1 組替財務諸表の作成手順
第2章	49頁	S4.2 等比数列の和の公式
第3章	95頁
第7章	314頁
第2章	54頁	S4.3 ポートフォリオの期待値，及び分散の導出
第2章	73頁	S4.4 CAPMの第二命題の証明
第2章	75頁	S4.5 $N$資産が投資可能な場合の最適ポートフォリオ問題
第7章	319頁
	327頁
	334頁
第3章	78頁	S4.6 Rの実行環境の準備
第3章	78頁	S4.7 クラウド上でRを実行する方法
第3章	90頁	S4.8 RStudio上で図表に日本語を挿入する方法
第7章	298頁	S4.9 任意の線形ファクター・モデルに関する一般化
第7章	321頁	S4.9 任意の線形ファクター・モデルに関する一般化
第7章	311頁	S4.10 会計情報ベースの株式価値評価モデル

S4.1 組替財務諸表の作成手順

ここでは，実際の一般事業会社を対象にして組替B/Sと組替P/Lを利用して分析ができるようになることを目的として，一般様式のB/SとP/Lを事業活動と金融活動を明確に区別して組み替える手順を説明しよう．

仮想企業を例にしたB/Sの組替手順

現実の企業のB/SやP/Lの項目は多岐にわたる上，業種によって登場する項目も異なる．そこで，現実の企業の組替手順を説明する事前準備として，いずれの企業のB/SやP/Lでも登場する項目のみの財務諸表を持つ仮想的な企業を例にして，組替手順を説明していこう．まずは，以下の図4.1に示された一般様式のB/Sの組替手順を説明する．

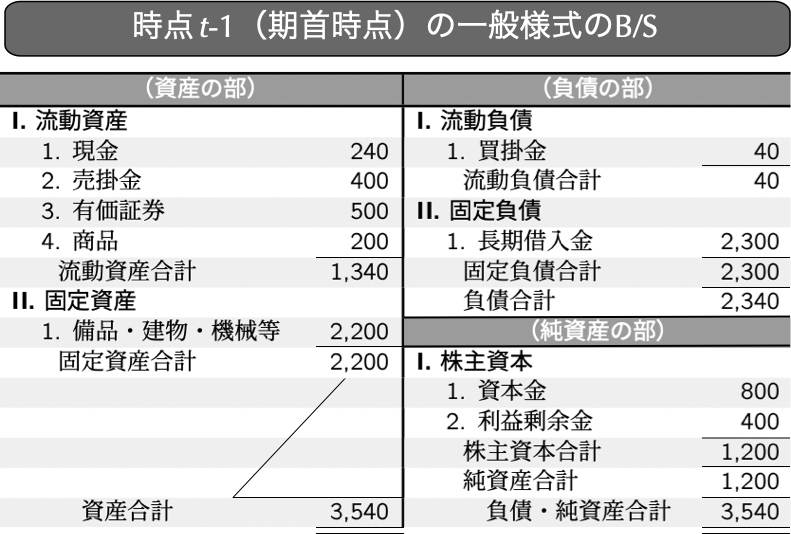
図4.1: 仮想企業の一般様式のB/S

上記で示した一般様式のB/Sの資産と負債のそれぞれを事業と金融とに区別したのが，次の図4.2の左側であり，それを踏まえて組み替えられたB/Sは，図4.2の右側である．

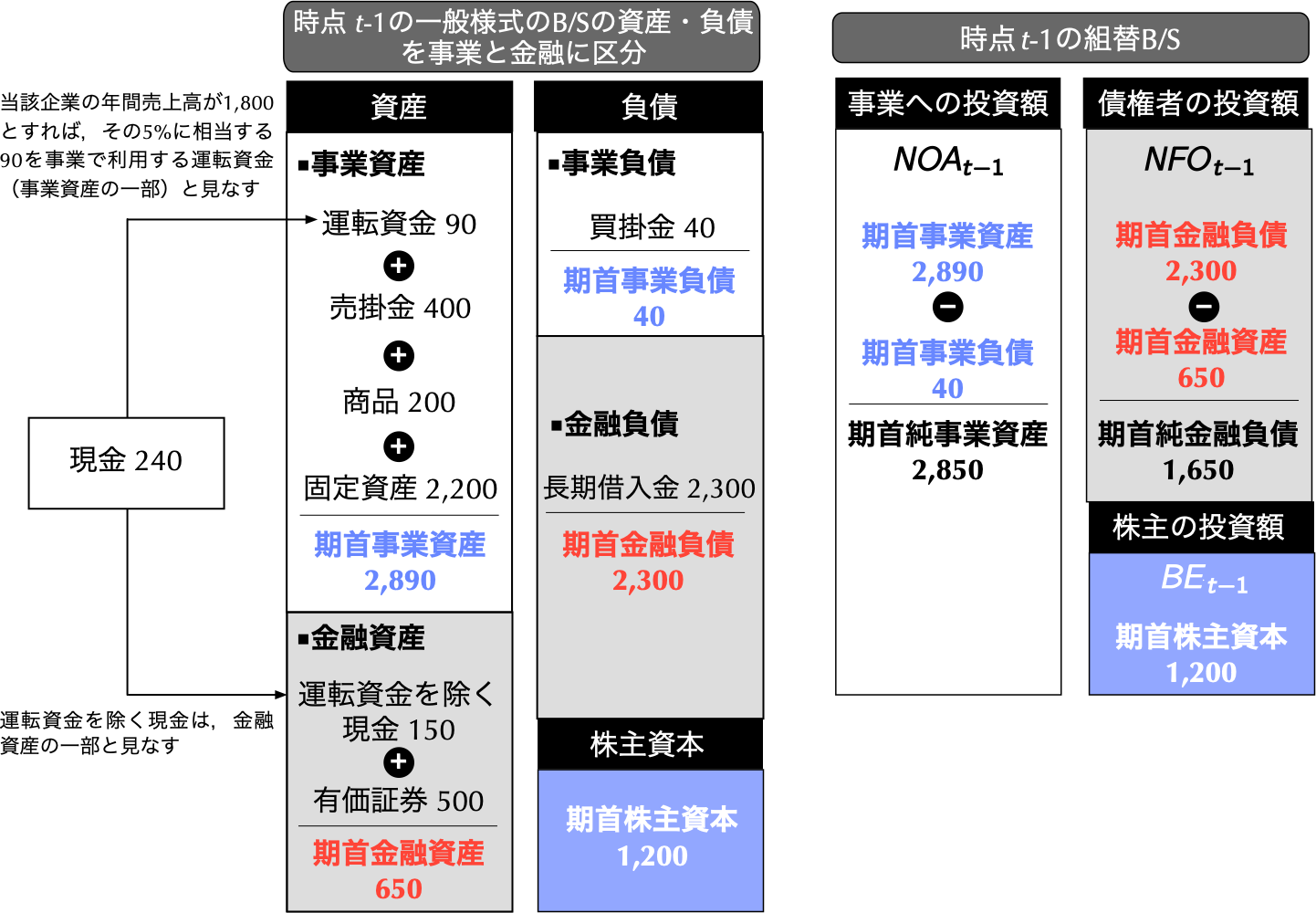
図4.2: 金融と事業を区別した一般様式のB/S（左側）と組替後のB/S（右側）

こうした組替B/Sを作成する一般的な手順について，以下では順を追って説明していこう．

[手順1] 金融資産と金融負債を先に定義する．その理由は，多くの一般事業会社の場合，資産と負債に共通して，事業項目に比して金融項目の方が相対的に少ないからである．そのため，金融資産と金融負債を先に決めてしまえば，資産合計（負債合計）から金融資産（金融負債）を差し引くことによって容易に事業資産（事業負債）を求められるという利点がある．

当該企業を例に，まずは金融資産を定義しよう．金融資産とは，金融投資によって保有する資産である（本文25頁）．したがって，その典型的な項目として「有価証券 500」がある．分類が悩ましいのが，現金である．現金の全額を金融資産として分類する方法も考えられるが，Penman (2012)^[6]や太田 (2018)^[7]など財務諸表分析の教科書では，事業活動を日々行うのにあたって決済用に保有している運転資金相当については，事業資産へと割り振り，残額の現金を金融資産として分類する案を推奨している．こうした現金の取扱方法といった細かな点から組替の手順といった本質的な点に至るまで，定石は存在せず，論者によって組替方法は異なる．例えば，Lundholm and Sloan (2019)^[4]は売上高の3%を，Penman (2012)^[6]は売上高の0.5%を運転資金とするのが一般的であると論じている．したがって，このサポートサイトで解説する方法もあくまで一つの例に過ぎない．実際の組替にあたっては，分析の目的や内容に応じて，各自にとって最善のやり方を模索してほしい．
太田 (2018)^[7]では，年間の売上高の5%相当を運転資金として事業資産に分類し，現金残高から運転資金を差し引いた残額を金融資産に分類する方法が提案されている ¹ ．ここでもその文献に従って，年間の売上高の5%を運転資金とする方法を採用してみよう．すなわち，当該企業の平均的な年間売上高が1,800だとすれば，その5%に相当する90は運転資金として事業資産へと割り振り，現金残高240のうち，運転資金90を除いた150は金融資産へと割り振るのである．したがって，金融資産は，有価証券に加えて，ここで計算された運転資金を除く現金残高を足し合わせて，次のように計算することができる． \[ \text{期首金融資産} = \underbrace{\text{運転資金を除く現金}}_{\textbf{240 $-$ 90}} + \underbrace{\text{有価証券}}_{\textbf{500}} = 650 \]
次に，金融負債を定義しよう．金融負債とは，資金調達を意図して背負った負債である．例の企業の場合，長期借入金の2,300がそれにあたる． \[ \text{期首金融負債} = \underbrace{\text{長期借入金}}_{\textbf{2,300}} = 2,300 \]

[手順2] 金融負債から金融資産を控除することによって純金融負債を算定する．

前述の[手順1]で算出された金融負債と金融資産から期首時点の純金融負債$\mathit{NFO}_{t-1}$が算定可能である． \[ \mathit{NFO}_{t-1} = \underbrace{\text{期首金融負債}}_{\textbf{2,300}} - \underbrace{\text{期首金融資産}}_{\textbf{650}} = 1,650 \]
一方，組替B/Sの右下のボックスに相当する期首株主資本$\mathit{BE}_{t-1}$については，一般様式のB/Sの株主資本をそのまま移行すれば良いので，これで組替B/Sの貸方（右側）が全て埋まることになる．

[手順3] 組替B/Sも一般様式のB/Sと同様，左右の合計額は一致する．組替B/Sの左右の関係を表す関係式，すなわち，純事業資産 $=$ 純金融負債 $+$ 株主資本を利用して，純金融負債に株主資本を足し合わせて，純事業資産を求め，組替B/Sを完成させる．この関係式を利用することにより，上の図の左側のように事業資産や事業負債の内容を事細かに定義せずとも，純事業資産を簡単に算定することができるというメリットがある．

したがって，例の企業であれば，期首時点の純事業資産$\mathit{NOA}_{t-1}$は，次のように計算することができる． \[ \mathit{NOA}_{t-1} = \underbrace{\mathit{NFO}_{t-1}}_{\textbf{1,650}} + \underbrace{\mathit{BE}_{t-1}}_{\textbf{1,200}} = 2,850 \]

仮想企業を例にしたP/Lの組替手順

続いて，以下で示す一般様式のP/Lを組み替える手順を説明しよう．なお，P/Lについては本文で解説したような収益と費用，当期純利益を左右対照表示する勘定式（図4.3の左側）と，収益の典型的な項目である売上高から始まり，種々の収益・費用を加減算することによって，ボトムラインによって当期純利益を配置する報告式（図4.3の右側）の二つがある．報告式P/Lでは，年間の経済活動を通じて最終的に獲得した当期純利益のみならず，本業の経済活動に限定した利益である営業利益や税コストを控除する前の経済活動全般の利益に相当する税引前当期純利益などが段階的に記される．こうした段階的利益計算により，どのような活動を通じて，どれだけの利益を獲得することができたかという利益の獲得過程を追うことができるようになるのである．有価証券報告書で開示されるのは報告式P/Lであり，組替手順をより深く理解するために，勘定式に加えて，報告式もここでは掲載している²．

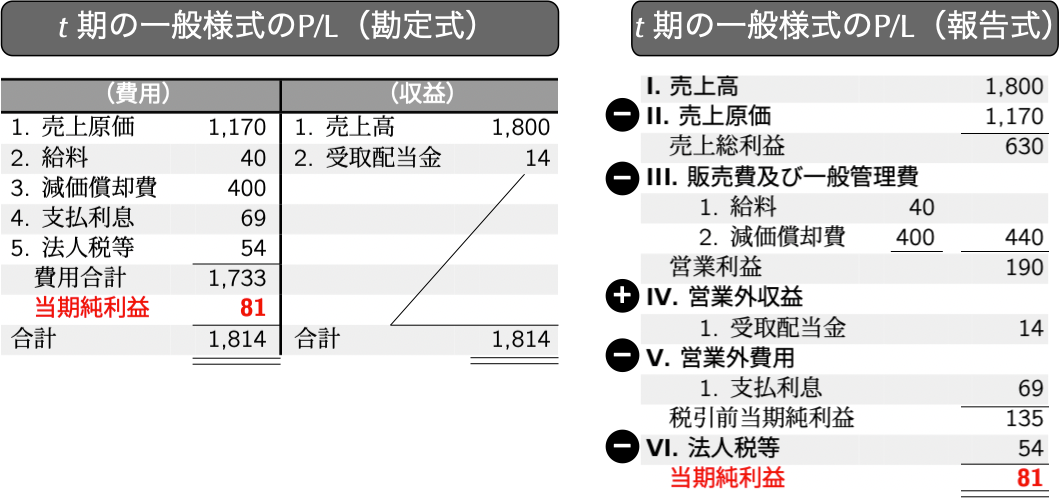
図4.3: 一般様式の勘定式P/L（左側）と報告式P/L（右側）

ここからは，一般様式の勘定式P/Lをベースに，組替P/Lの作成手順を説明していこう．

[手順1] 組替にあたっては，税金の取扱いに細心の注意を払う必要がある．そこで，まずはP/Lの費用に計上される法人税等の54を一旦取り除き，税金を無視したP/Lを考え，収益と費用のそれぞれの項目を事業と金融に区分しよう（区分後のP/Lは，以下の図4.4の左側）．そのために，組替B/Sと同様に，金融に関連するもの（金融収益と金融費用）を先に定義する．

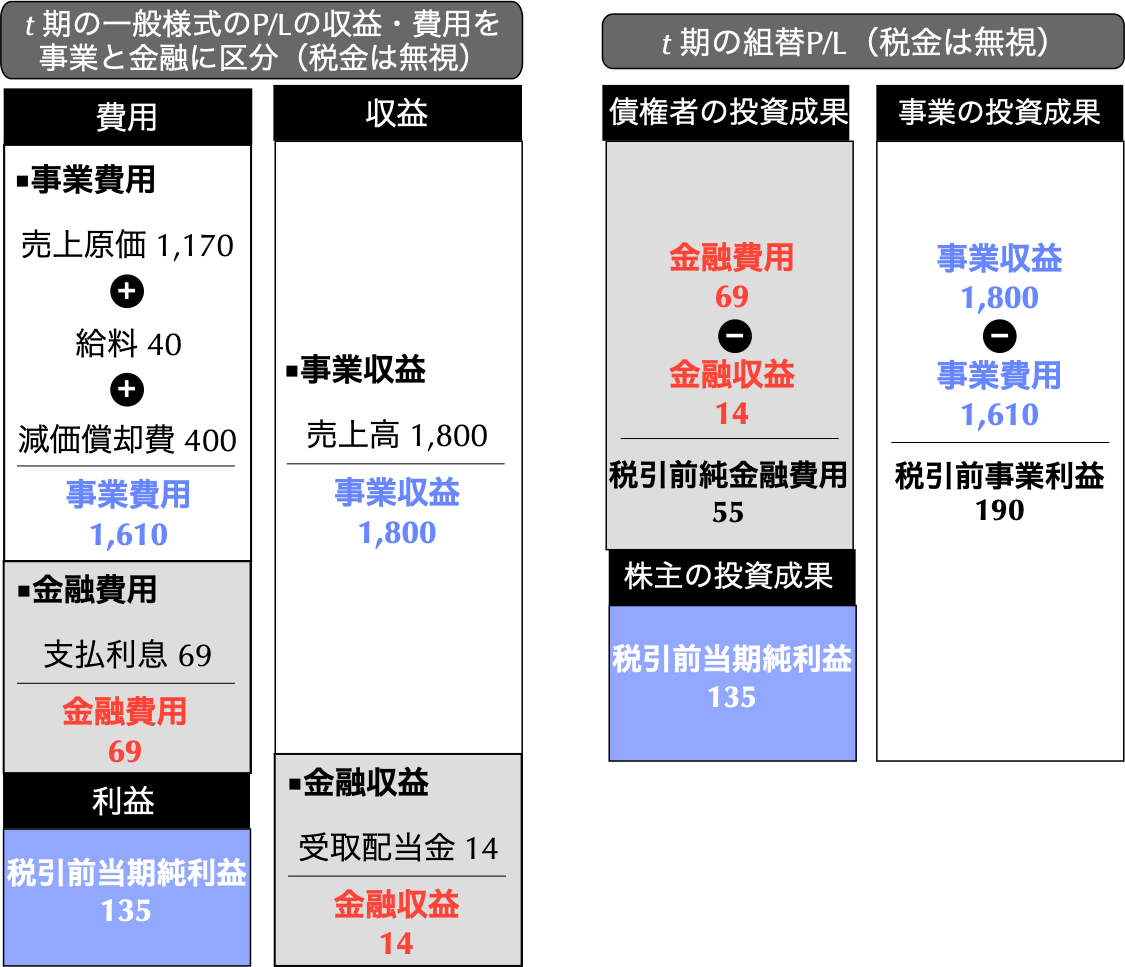
図4.4: 金融と事業を区別した税金を無視した一般様式のP/L（左側）と税金を無視した組替後のP/L（右側）

金融費用とは金融負債から派生する費用であり，長期借入金という金融負債を背負っていたことに伴って負担した支払利息69がそれに相当する．他方，金融収益とは，金融資産から派生した収益であり，有価証券という金融資産を保有していたからこそ実現した受取配当金14がそれに相当する．

[手順2] 金融費用から金融収益を控除することによって純金融費用を算定する．

前述の[手順1]で算出された金融費用と金融収益から期中の純金融費用が算定可能である．ただし，ここでの純金融費用は，税金を無視しているという意味で，税引前純金融費用であることに注意されたい．こうして算出された税引前純金融費用が税金を無視した組替P/L（上記の図4.4の右側）に配置される． \[ \text{税引前純金融費用} = \underbrace{\text{金融費用}}_{\textbf{69}} - \underbrace{\text{金融収益}}_{\textbf{14}} = 55 \]
一方，税金を無視した組替P/Lの左下のボックスに相当する税引前当期純利益については，報告式P/Lの税引前当期純利益をそのまま移行すれば良いので，これで組替P/Lの借方（左側）が全て埋まることになる．

[手順3] 税引前であろうが，税引後であろうが，組替P/Lにおいては，当期純利益 $=$ 事業利益 $-$ 純金融費用 $\Longleftrightarrow$ 純金融費用 $+$ 当期純利益 $=$ 事業利益が成立する．したがって，税金を無視した組替P/Lを考える場合，税引前純金融費用に税引前当期純利益を足し合わせることによって税引前事業利益が算定可能である．この関係式を利用することにより，図4.4の左側のように事業収益や事業費用の内容を事細かに定義せずとも，税引前事業利益を容易に算定できる．

\[ \text{税引前事業利益} = \underbrace{\text{税引前純金融費用}}_{\textbf{55}} + \underbrace{\text{税引前当期純利益}}_{\textbf{135}} = 190 \]

[手順4] 税率をベースに，各項目とも税引後に調整し，税金を考慮した（税引後）組替P/Lを完成させる．

例えば，税率を40%と仮定する³と，各項目について，税引前数値，税金，税引後数値との関係は，次の通りである．

	事業利益	純金融費用	当期純利益
① 税引前	$190$	$55$	$135$
② 税金 ($=$ ① $\times$ 40%)	$76$	$22$	$54$
税引後 ($=$ ① $-$ ②)	$\underbrace{114}_{OX_{t}}$	$\underbrace{33}_{NFE_{t}}$	$\underbrace{81}_{X_{t}}$

事業利益や当期純利益については，稼いだ税引前利益に対して税率の40%が税金として課せられるため，税引後利益はそれぞれ114と81となり，これが本文で$\mathit{OX}_{t}$と$X_{t}$と表現していたものに相当する．特に税引後の当期純利益は，一般様式のP/Lに計上されている当期純利益の金額と一致するのがポイントである．
他方，純金融費用については，税引前の金額に比べて，税引後の金額の方が少なくなっていることに戸惑うかもしれない．これは，純金融負債によって資金調達を行い，それに伴って純金融費用のコスト負担を強いられることによって，国・地方公共団体から税引前純金融費用に税率を掛け合わせた分だけ補助金を受けることができたと考えれば良い．この補助金におかげで，実質的に負担しなければならない純金融費用は軽減されることなるのである．補助金に相当する額は，負債の節税効果 (tax shield/tax benefit)と呼ばれ，以下の計算式によって求められる． \[ \text{負債の節税効果} = \text{税引前純金融費用} \times \text{税率} \]
この負債の節税効果に相当する金額だけ純金融費用の負担は軽減されることになるので，実質的な純金融費用，すなわち，税引後純金融費用$\mathit{NFE}_{t}$は，次のように計算することができる． \[ \begin{align} \mathit{NFE}_{t} & = \text{税引前純金融費用} - \text{税引前純金融費用} \times \text{税率} \nonumber\\ & = (1 - \text{税率}) \times \text{税引前純金融費用} \tag{4.1} \end{align} \]

したがって，当該企業の税引後純金融費用$\mathit{NFE}_{t}$は$(1 - 40\%) \times 55 = 33$である．

なお，実践上，税引後事業利益に相当する$\mathit{OX}_{t}$については，以下の組替P/Lの関係式を利用すれば良いので，事業収益や事業費用，事業利益に課せられる税金がいくらかをわざわざ考える必要がない．税引前純金融費用は，金融費用と金融収益から算出できるし，他方，$X_{t}$は，一般様式の当期純利益をそのまま代入すれば良い． \[ \underbrace{NFE_{t}}_{(1 - \text{税率}) \times \text{税引前純金融費用}} + X_{t} = OX_{t} \]

こうして，本文図1.11（30頁）で示した組替B/Sと組替P/Lのすべての項目が下記の図4.5のように埋まることになる．

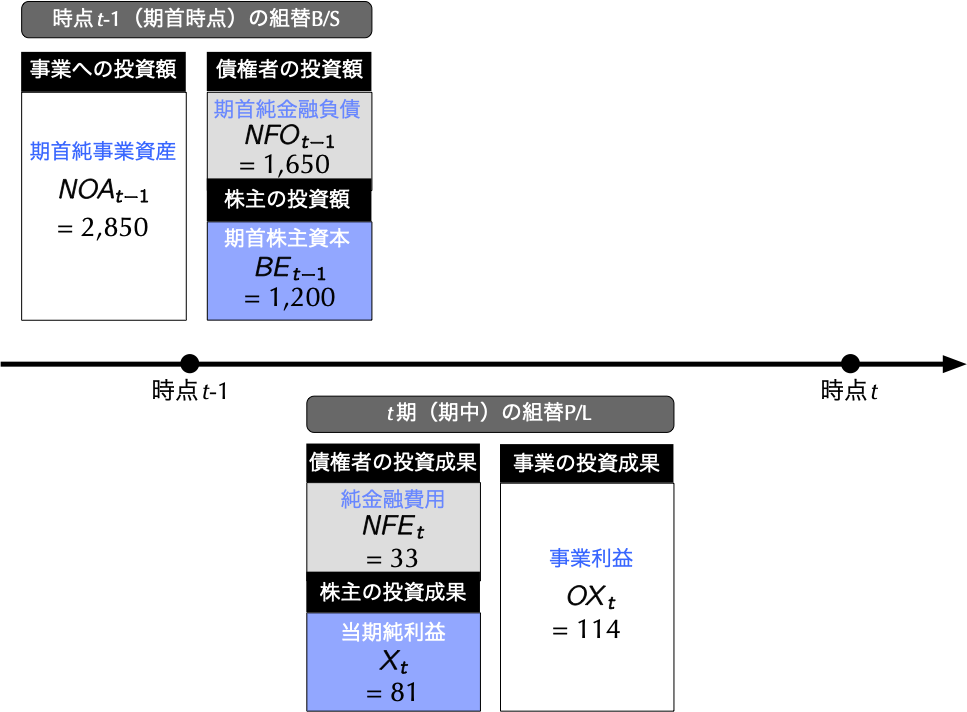
図4.5: 時点$t-1$の組替B/Sと$t$期の組替P/L

したがって，当該企業の$t$期における会計上の事業のリターン$\mathit{RNOA}_{t}$，債権者のリターン（企業にとっての借入コスト）$\mathit{NBC}_{t}$，株主のリターン$\mathit{ROE}_{t}$は，それぞれ次のように計算することができる． \[ \begin{align*} \mathit{RNOA}_{t} & = \frac{114}{2,850} = 4\% \\ \mathit{NBC}_{t} & = \frac{33}{1,650} = 2\% \\ \mathit{ROE}_{t} & = \frac{81}{1,200} = 6.75\% \end{align*} \]

実際の一般事業会社を想定した財務諸表の組替手順

ここまで仮想企業を例に組替B/Sと組替P/Lの作成方法を説明してきたが，その手順のポイントをまとめると次のように要約することができる．

B/Sの組替にあたっては，金融資産と金融負債を定義することにより純金融負債が算定でき，あとはB/Sの株主資本とそれを足し合わせて純事業資産を導出する．
P/Lの組替にあたっては，金融収益と金融費用を定義することにより税引前純金融費用が算定でき，次に，負債の節税効果を考慮して税引後純金融費用を計算する．その後，税引後純金融費用に当期純利益を足し合わせて税引後事業利益を求める．

したがって，仮想企業に限らず，実際の一般事業会社についてもB/Sの金融資産・負債，及びP/Lの金融収益・費用の金融項目さえ定義することができれば，簡単に組替B/Sと組替P/Lを作成することができる．以下では，日本企業を対象にした実証会計・ファイナンス研究において，最も頻用されるデータベースの一つである日本経済新聞社のFinancialQUESTを例に，金融項目の計算過程を例示しよう．括弧内は，そのデータベース上での各項目のコードである．なお，現金・預金については，全額を金融資産として分類する簡便的なやり方を前提にしているが，仮想企業の例で説明したように，適当な金額を運転資金として事業資産に割り振るのも一案である．もちろん，以下の計算過程は，一つの案に過ぎず，分析の目的や内容に応じて取捨選択したり，項目を追加したりしてほしい．

項目	計算過程
金融資産	現金・預金 (B01022) $+$ 有価証券 (B01033) $+$ 短期貸付金 (B01051) $+$ 金銭の信託 (B01055) $+$ デリバティブ債権 (B01056 $+$ B01100) $+$ 繰延ヘッジ損失 (B01057) $+$ 自己株式 (B01058) $+$ 長期貸付金 (B01091) $+$ 投資不動産 (B01096) $-$ 繰延ヘッジ損益 (C01100)
金融負債	短期借入金・社債合計 (C01026) $+$ リース債務 (C01035 $+$ C01064) $+$ デリバティブ債務 (C01043 $+$ C01075) $+$ 繰延ヘッジ利益 (C01076) $+$ 従業員預り金 (C01047) $+$ 長期借入金・社債・転換社債 (C01058) $+$ 長期支払手形 (C01065) $+$ 長期未払金 (C01066)
金融収益	受取利息・配当金 (D01031 or D01163) $+$ 有価証券売却益 (D01034) $+$ 有価証券評価益 (D01035) $+$ デリバティブ評価益 (D01036)
金融費用	支払利息・割引料 (D01047 or D01166) $+$ 有価証券売却損 (D01053) $+$ 有価証券評価損 (D01054) $+$ デリバティブ評価損 (D01055)

B/Sについて，上記の計算過程に従い，金融負債から金融資産を差し引き，純金融負債を導出し，あとは株主資本を足し合わせれば純事業資産を導出することができる．なお，株主資本については，各企業が採用する会計基準ごとに次のように算出する方法が一案である．

日本基準: 自己資本 (C01106) $-$ 評価・換算差額等 (C01098)⁴
SEC基準: 自己資本 (C01106) $-$ その他の包括利益累計額 (C01108)
IFRS基準: 親会社の所有者に帰属する資本 (C01106) $-$ 累積その他の包括利益 (C01098)

他方，P/Lについて，上記の計算過程により，金融費用から金融収益を差し引き，税引前純金融費用を導出する．そして，(4.1)式に従って，税引後純金融費用を算定する．この際，仮想企業の例では，外生的に40%の税率を与えていたが，実践上は分析者自身が適切な値を決めなければならない．ここでの税率は厳密に言うと，限界税率 (marginal tax rate) ⁵ と呼ばれるものであるが，実践上は，法定実効税率で代用することが多い．法定実効税率については，財務省の財務総合政策研究所が発刊する「財政金融統計月報」によりデータを入手し，加工することによって長期の系列を入手することが可能である．2021年時点における法定実効税率（財務省型）は，約29.74%である⁶．なお，赤字企業や過去からの繰越欠損があるような企業については，税コストの負担がなく，負債の節税効果を享受することができないので，より厳密に税率をゼロとするのも一案である．

こうして税引前純金融費用と適切な限界税率から(4.1)式により税引後純金融費用が得られれば，あとはそれに親会社株主に帰属する当期純利益/当期利益[累計] (D01110)を加えれば，税引後事業利益を求めることができる．

以上の流れを踏むことにより，組替B/Sと組替P/Lを作成することができ，それらの財務諸表をベースにして企業分析を遂行することが可能である．

S4.2 等比数列の和の公式

本文第3章で毎年のキャッシュフローが等しい場合のNPVを計算したことを思い出そう（94頁）．ここでは，その際に用いた等比数列の和の公式を一般的に導出する．この公式は，コーポレート・ファイナンスの文脈で頻出し，企業価値を計算する際に登場する永続価値や，毎年一定額の給付を受け取れる年金 (annuity)の現在価値などを計算する際に応用される．

初項を$a_1$，公比を$g$とする等比数列$a_t$を考えよう．この等比数列の各要素は一般的に$a_t=a_1g^{t-1}$と書ける．この等比数列の初項から$T$番目までの要素の合計$S_T$を求めたい．

\[ S_T=\sum_{t=1}^{T}a_t=\sum_{t=1}^{T}{a_1g^{t-1}} \]

ここで，$gS_T$を計算してみると，

\[ gS_T=\sum_{t=1}^{T}{a_1g^t}=\sum_{t=2}^{T+1}a_t=S_T+a_{T+1}-a_1 \]

と書き換えられるので，$g\neq1$の時に上式を$S_T$に関して解くことができる．

\[ S_T=\frac{a_1-a_{T+1}}{1-g}=\frac{a_1\left(1-g^T\right)}{1-g} \]

また，$|g|<1$の時，$\displaystyle \lim_{T\rightarrow\infty}{g^T}=0$であるから，無限等比数列の和（等比級数）も計算することができて，

\[ \lim_{T\rightarrow\infty}{S_T}=\sum_{t=1}^{\infty}a_t=\frac{a_1}{1-g} \]

これらの公式をファイナンスに応用する際，初年度のキャッシュフローを$\mathit{CF}_1$，割引率を$\widetilde{R}$として，初項$a_1$が$\frac{\mathit{CF}_1}{1+\widetilde{R}}$，公比$g$が$\frac{1}{1+\widetilde{R}}$であることが多い（実際，本文第3章の例ではこの形で用いた）．これらの定義を上式に代入すると，以下のように書き換えられる．

\[ S_T=\frac{\frac{\mathit{CF}_{1}}{1+\widetilde{R}}\left(1-\left(\frac{1}{1+\widetilde{R}}\right)^T\right)}{1-\frac{1}{1+\widetilde{R}}}=\frac{\mathit{CF}_1}{\widetilde{R}}\left(1-\left(\frac{1}{1+\widetilde{R}}\right)^T\right) \]

\[ \lim_{T\rightarrow\infty}{S_T}=\frac{\mathit{CF}_1}{\widetilde{R}} \]

S4.3 ポートフォリオの期待値，及び分散の導出

本文第2章で銘柄AとBから構成されるポートフォリオの期待値，及び分散を以下のように表現したことを思い出そう（54頁）．

\[ \begin{align} &\mu_{P} = w_{A}\mu_{A} + w_{B}\mu_{B}\\ &\sigma_{P}^2 = w_{A}^2\sigma_{A}^2 + w_{B}^2\sigma_{B}^2 + 2\rho w_{A}w_{B}\sigma_{A}\sigma_{B} \end{align} \]

ここで，$w_{A}$，及び$w_{B}$は両者の保有比率である．これらの式は，ポートフォリオのリターンが$R_{P} = w_{A}R_{A} + w_{B}R_{B}$と書けることと，期待値，及び分散の定義から導出できる．まず，期待値の線形性より，

\[ \mu_{P} = \mathbb{E}\left[R_{P}\right] = \mathbb{E}[w_{A}R_{A} + w_{B}R_{B}] = w_{A}\mathbb{E}[R_{A}] + w_{B}\mathbb{E}[R_{B}] = w_{A}\mu_{A} + w_{B}\mu_{B} \] である．一方，分散はもう少し複雑で，

\[ \sigma_{P}^2 = {\rm Var}[R_{P}] = {\rm Var}[w_{A}R_{A} + w_{B}R_{B}] = \mathbb{E}[(w_{A}R_{A} + w_{B}R_{B})^2]-\mathbb{E}[w_{A}R_{A} + w_{B}R_{B}]^2 \] 第一項と第二項をそれぞれ計算してみると，

\[ \begin{align} &\mathbb{E}[\left(w_{A}R_{A} + w_{B}R_{B}\right)^2] = w_{A}^2\mathbb{E}[R_{A}^2] + w_{B}^2\mathbb{E}[R_{B}^2] + 2w_{A}w_{B}\mathbb{E}[R_{A}R_{B}]\\ &\mathbb{E}[w_{A}R_{A} + w_{B}R_{B}]^2 = w_{A}^2\mathbb{E}[R_{A}]^2 + w_{B}^2\mathbb{E}[R_{B}]^2 + 2w_{A}w_{B}\mathbb{E}[R_{A}]\mathbb{E}[R_{B}] \end{align} \] これらを整理して，

\[ \begin{align} &\sigma_{A}^2 = {\rm Var}[R_{A}] = \mathbb{E}[R_{A}^2]-\mathbb{E}[R_{A}]^2\\ &\sigma_{B}^2 = {\rm Var}[R_{B}] = \mathbb{E}[R_{B}^2]-\mathbb{E}[R_{B}]^2\\ &\rho\sigma_{A}\sigma_{B} = {\rm Cov}[R_{A},R_{B}] = \mathbb{E}[R_{A}R_{B}]-\mathbb{E}[R_{A}]\mathbb{E}[R_{B}] \end{align} \] の定義式を用いると，ポートフォリオの分散に関する式が得られる．

以下の図4.6と図4.7では，銘柄AとBに投資するポートフォリオの期待リターン$\mu_{P}$，及び分散$\sigma_{P}^{2}$を，銘柄Bの保有比率$w_{B}$の関数として描いている．各銘柄の期待リターンや分散，相関係数は本文第2章の数値例をそのまま用いている．

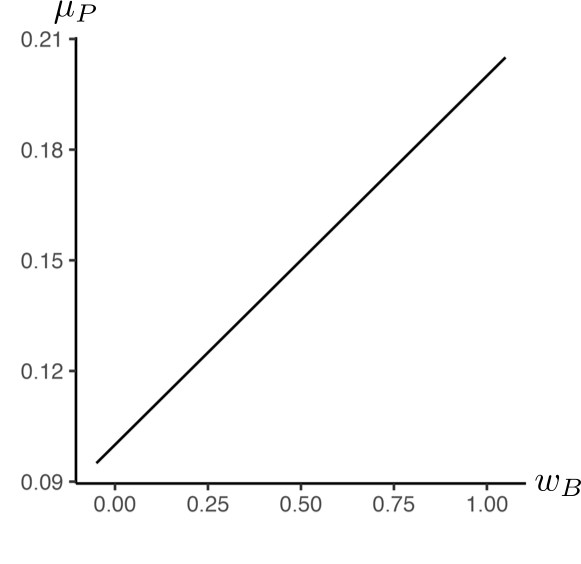
図4.6: 銘柄Bの保有比率$w_{B}$とポートフォリオの期待リターン$\mu_{P}$の関係

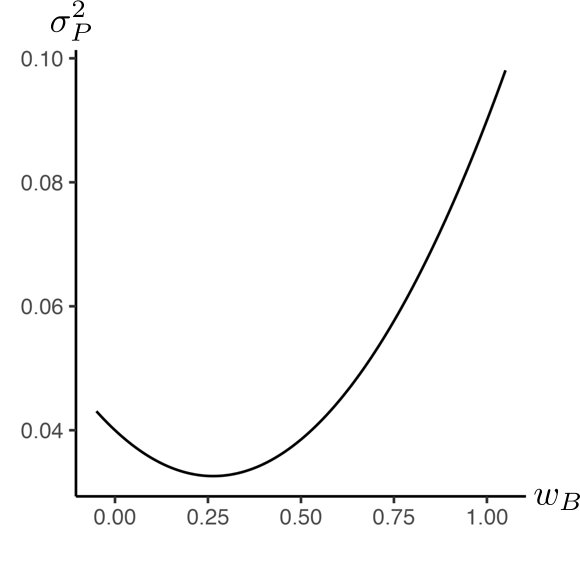
図4.7: 銘柄Bの保有比率$w_{B}$とポートフォリオの分散$\sigma_{P}^{2}$の関係

S4.4 CAPMの第二命題の証明

任意の証券$i$を固定し，市場ポートフォリオを$1-\alpha$，証券$i$を$\alpha$の比率でそれぞれ保有するポートフォリオを考える．CAPMの第一命題によると，このポートフォリオは$\alpha=0$で市場ポートフォリオと一致して効率的となるが，それ以外は非効率的となる．このポートフォリオの期待リターンと標準偏差をそれぞれ$\mu(\alpha)$と$\sigma(\alpha)$で表し，$\alpha$を動かしたときに$(\mu(\alpha),\sigma(\alpha))$が描く軌跡を$C_i$と呼ぶ．曲線$i$は$\alpha=0$の時に資本市場線上にある一方，$\alpha\neq0$の時に資本市場線の内側に位置する．

サポートサイトS4.5節の数値例をもとに，資本市場線と$C_i$の関係を図示したのが以下の図4.8と図4.9である．この数値例では危険資産が三つあり，各証券，三資産の平均分散フロンティア，市場ポートフォリオ，及び資本市場線は図4.8のように描画できる．ただし，無リスク金利は1%としている．

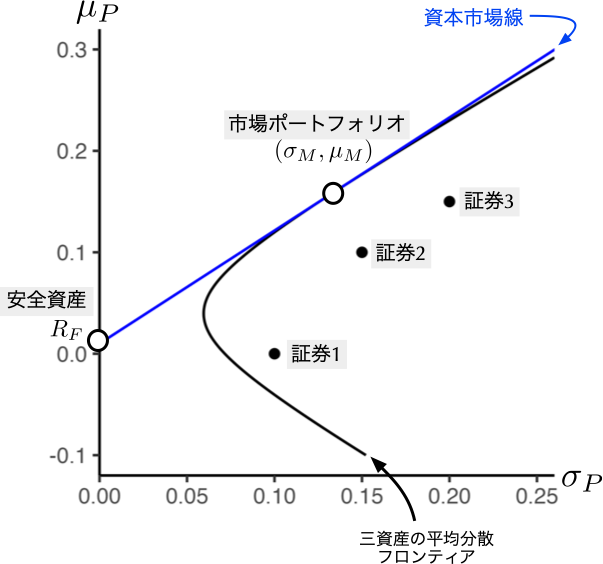
図4.8: 三証券を前提にしたリスク・リターン平面（$R_{F}$は無リスク金利を，$\mu_{M}$と$\sigma_{M}$はそれぞれ市場ポートフォリオの期待リターンと標準偏差を表す）

続いて，証券1を例に，その証券に対する保有割合$\alpha$を変化させたときの軌跡$C_1$を描いたのが次の図4.9であり，$\alpha = 0$のとき，$C_1$が資本市場線と接する様子を見てとれる．

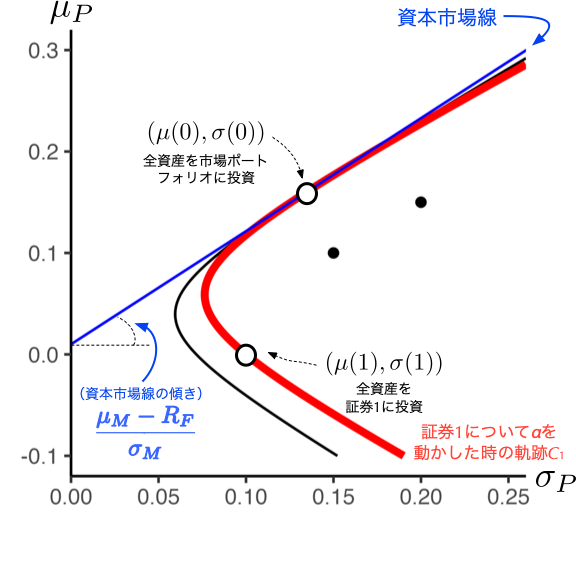
図4.9: 証券1について保有比率$\alpha$を変化させた場合の軌跡$C_{1}$

任意の証券$i$について，$C_i$と資本市場線がこのような位置関係になるためには，両者の傾きが$\alpha=0$で一致する必要がある．まず資本市場線の傾きは市場ポートフォリオのシャープ・レシオである． \[ \frac{\mu_M-R_F}{\sigma_M} \]

一方，$C_i$の傾きは$\mu(\alpha)$と$\sigma(\alpha)$の$\alpha$に関する微係数の比率として計算できる． \[ \left.\frac{d\mu(\alpha)}{d\alpha}\middle/\frac{d\sigma(\alpha)}{d\alpha}\right|_{\alpha=0} \]

ここで，市場ポートフォリオと証券$i$の相関係数を$\rho_{Mi}$とおくと， \[ \begin{align} \frac{d\mu\left(\alpha\right)}{d\alpha}&=\frac{d}{d\alpha}\left(\left(1-\alpha\right)\mu_M+\alpha\mu_i\right)=\mu_i-\mu_M\\ \frac{d\sigma\left(\alpha\right)}{d\alpha}&=\frac{d}{d\alpha}\left(\left(1-\alpha\right)^2\sigma_M^2+\alpha^2\sigma_i^2+2\alpha\left(1-\alpha\right)\rho_{Mi}\sigma_M\sigma_i\right)^\frac{1}{2}\\ &=\frac{-\left(1-\alpha\right)\sigma_M^2+\alpha\sigma_i^2+\left(1-2\alpha\right)\rho_{Mi}\sigma_M\sigma_i}{\sqrt{\left(1-\alpha\right)^2\sigma_M^2+\alpha^2\sigma_i^2+2\alpha\left(1-\alpha\right)\rho_{Mi}\sigma_M\sigma_i}} \end{align} \] であるから， \[ \left.\frac{d\mu(\alpha)}{d\alpha}\middle/\frac{d\sigma(\alpha)}{d\alpha}\right|_{\alpha=0}=\frac{\mu_i-\mu_M}{{(-\sigma_M^2+\rho_{Mi}\sigma_M\sigma_i)/\sigma_M}}=\frac{\mu_i-\mu_M}{\rho_{Mi}\sigma_i-\sigma_M} \] と計算できる．したがって，$C_i$と資本市場線の傾きが一致する条件から， \[ \begin{align} \frac{\mu_M-R_F}{\sigma_M}=\frac{\mu_i-\mu_M}{\rho_{Mi}\sigma_i-\sigma_M}&\Longleftrightarrow(\rho_{Mi}\sigma_i-\sigma_M)(\mu_M-R_F)=\sigma_M(\mu_i-\mu_M)\\ &\Longleftrightarrow \ \mu_i-R_F=\frac{\rho_{Mi}{\sigma_M\sigma}_i}{\sigma_M^2}(\mu_M-R_F) \end{align} \] （証明終わり）

ちなみに，本書のレベルを超えるので詳しくは説明しないが，CAPMの本質は確率的割引因子 (stochastic discount factor)が市場ポートフォリオのリターンに関して線形関数として表現できることである．それさえ分かれば，CAPMの第二命題は確率的割引因子の定義式を書き換えるだけで簡単に証明できる．詳しくは，例えば Cochrane (2009)^[2]のChapter 9を参照してほしい．

S4.5 $N$資産が投資可能な場合の最適ポートフォリオ問題

本節では本文第2章で紹介した平均分散アプローチを危険資産が$N$個ある場合に拡張し，最適ポートフォリオを解析的に導出してみよう．ここでは$N$個全てが危険資産だと想定して議論を進めるが，安全資産を追加すると有効フロンティアは危険資産が2個のみの場合と同様に直線となる．

各資産の保有比率を$N$次元の縦ベクトル$\boldsymbol{w}$で表す．ここで$w$の$i$番目の要素$w_i$は証券$i$の保有比率を表す． \[ \boldsymbol{w} = \left(\begin{matrix}w_1\\\vdots\\w_N\\\end{matrix}\right) \]

定義により保有比率は合計が1になる．従って，各要素が1である$N$次元の縦ベクトルを$\boldsymbol{1_N}$で表すと，以下が成立する． \[ \boldsymbol{w^\prime} \boldsymbol{1_N}=w_1+\cdots+w_N=1 \]

さて，投資対象の$N$資産の期待リターンを$\boldsymbol{\mu}$，分散共分散行列を$\boldsymbol{\Sigma}$で表す．ここで，$\boldsymbol{\mu}$は$N$次元の縦ベクトルであり，$i$番目の要素$\mu_i$は証券$i$の期待リターンを表す． \[ \boldsymbol{\mu} = \left(\begin{matrix}\mu_1\\\vdots\\\mu_N\\\end{matrix}\right) \]

一方，$\boldsymbol{\Sigma}$は$N\times N$次元の正方行列であり，$(i,j)$番目の要素$\sigma_{i,j}$は，$i = j$のときに証券$i$の分散を，$i\neq j$のときに証券$i$と$j$の共分散を表す． \[ \boldsymbol{\Sigma}=\left(\begin{matrix}\sigma_{1,1}&\cdots&\sigma_{1,N}\\\vdots&\ddots&\vdots\\\sigma_{N,1}&\cdots&\sigma_{N,N}\\\end{matrix}\right) \]

分散共分散行列$\boldsymbol{\Sigma}$を所与とすると，任意の保有比率$\boldsymbol{w}$に対してポートフォリオの分散は二次形式で表現できる． \[ \boldsymbol{w^\prime \Sigma w}\ =\ \sum_{i}{w_i^2\sigma_{i,i}} + 2\sum_{i>j}{w_iw_j\sigma_{i,j}} \]

また，このポートフォリオの期待リターンは，各資産の期待リターン$\boldsymbol{\mu}$を用いて以下のように書ける． \[ \boldsymbol{w^\prime\mu} = w_1\mu_1+\cdots+w_N\mu_N \]

さて，任意の保有比率に対して期待リターン，及び分散が表現できたので，今度は効率的フロンティアの分析に移ろう．任意の目標期待リターン$\mu_0$に対して，$\mu_0$を実現するポートフォリオの中から分散を最小化するものを選ぶ最適化問題を考える．

\[ \begin{align} \min_\boldsymbol{w} &{\ \boldsymbol{w^\prime\Sigma w}}\\ \text{s.t.}\ \ \ & \boldsymbol{\mu^\prime w} = \mu_0\\ & \boldsymbol{1_N^\prime w} = 1 \end{align} \] ここで，s.t.はsubject toの略で，以下の制約式の下でという意味である．空売りを許容する場合，各資産の保有比率は負の値も含めた$N$次元のベクトルとなるが，目標期待リターン$\mu_0$を達成するという条件（第一式）と，各資産の保有比率の合計が1になるという条件（第二式）は満たす必要がある．ここでは$\mu_0$をパラメータとして扱っているので，最適ポートフォリオはその関数$\boldsymbol{w}(\mu_0)$として表現できる．そして，異なる$\mu_0$に対して最適ポートフォリオ$\boldsymbol{w}(\mu_0)$を求めれば，効率的フロンティアを導出することができる．

さて，実際に上の制約付き最適化問題を解いてみよう．本文第7章では数値的最適化によって最適ポートフォリオを求めたが，この問題には解析解が存在する．まずはラグランジュの未定乗数を導入し，制約付き最適化問題を制約無し最適化問題に書き換えよう． \[ \min_\boldsymbol{w}{\ \boldsymbol{w^\prime\Sigma w}}\ -\lambda(\boldsymbol{\mu^\prime w} - \mu_0)-\gamma(\boldsymbol{1_N^\prime w} - 1) \] それぞれ第二項と第三項に登場する$\lambda$と$\gamma$がラグランジュの未定乗数である．$\boldsymbol{w}$，$\lambda$，$\gamma$に関してそれぞれ一階条件を取ると，以下の連立方程式が得られる． \[ \begin{align} 2 \boldsymbol{\Sigma w} - \lambda\boldsymbol{\mu} - \gamma \boldsymbol{1_N} & = \boldsymbol{0_N}\\ \boldsymbol{\mu^\prime w} - \mu_0 & = 0\\ \boldsymbol{1_N^\prime w} - 1 & = 0 \end{align} \] ここで，最初の式は$N$次元のベクトル式になっていることに注意しよう．この式は上から順に，$\boldsymbol{w}$の各要素に関して目的関数を偏微分した係数が並んでいる．従って，この連立方程式は$N+2$次元であるが，未知変数も$\boldsymbol{w}$の各要素に$\lambda$と$\gamma$を加えてちょうど$N+2$個あるので，係数行列が正則である限り，一意に解を求めることができる．

まず，ラグランジュの未定乗数$\lambda$と$\gamma$を含む形で，$\boldsymbol{w}$に関して第一式を解く． \[ \boldsymbol{w} = \frac{1}{2}\boldsymbol{\Sigma}^{-1} \left(\lambda \boldsymbol{\mu} + \gamma \boldsymbol{1_N}\right) \]

これを第二式と第三式にそれぞれ代入する． \[ \begin{align} \frac{1}{2}\boldsymbol{\mu^\prime\Sigma}^{-1}\left(\lambda \boldsymbol{\mu} + \gamma \boldsymbol{1_N}\right) - \mu_0 & = 0\\ \frac{1}{2}\boldsymbol{1_N^\prime\Sigma}^{-1}\left(\lambda \boldsymbol{\mu} + \gamma \boldsymbol{1_N}\right) - 1 & =0 \end{align} \]

これを$\lambda$と$\gamma$に関して整理すると以下のように書き換えられる． \[ \left(\begin{matrix}\boldsymbol{\mu^\prime\Sigma}^{-1} \boldsymbol{\mu} & \boldsymbol{\mu^\prime\Sigma}^{-1} \boldsymbol{1_N} \\\boldsymbol{1_N^\prime\Sigma}^{-1} \boldsymbol{\mu} & \boldsymbol{1_N^\prime\Sigma}^{-1} \boldsymbol{1_N}\\\end{matrix}\right)\left(\begin{matrix}\lambda\\\gamma\\\end{matrix}\right)=2\left(\begin{matrix}\mu_0\\1\\\end{matrix}\right) \]

ここで，表記を簡単にするよう以下の変数を定義する．いずれもスカラー変数であることに注意しよう． \[ A = \boldsymbol{\mu^\prime\Sigma}^{-1}\boldsymbol{\mu};\ \ \ \ B = \boldsymbol{\mu^\prime\Sigma}^{-1} \boldsymbol{1_N};\ \ \ \ C = \boldsymbol{1_N^\prime\Sigma}^{-1}\boldsymbol{1_N} \] こうすると，二次元の正方行列の逆行列の公式を用いて，$\lambda$と$\gamma$を求めることができる． \[ \begin{align} \left(\begin{matrix}\lambda\\\gamma\\\end{matrix}\right)&=2\left(\begin{matrix}A&B\\B&C\\\end{matrix}\right)^{-1}\left(\begin{matrix}\mu_0\\1\\\end{matrix}\right)\\ &=\frac{2}{AC-B^2}\left(\begin{matrix}C&-B\\-B&A\\\end{matrix}\right)\left(\begin{matrix}\mu_0\\1\\\end{matrix}\right) \end{align} \] これを先ほどの$\boldsymbol{w}$の式に代入すると，最終的に以下の解が得られる． \[ \boldsymbol{w} = \boldsymbol{\Sigma}^{-1}\frac{\left(C\mu_0-B\right)\boldsymbol{\mu}+\left(A-B\mu_0\right)\boldsymbol{1_N}}{AC-B^2} \]

なお，ここでは一階の必要条件から最適ポートフォリオを導出したが，分散共分散行列$\boldsymbol{\Sigma}$が正定値であることから，二階の十分条件が満たされている．

（数値例） $N=3$とし，各銘柄の期待リターン及び標準偏差，相関係数がそれぞれ以下の通り表されるとしよう． \[ \begin{align} &\left(\begin{matrix}\mu_1\\\mu_2\\\mu_3\\\end{matrix}\right)=\left(\begin{matrix}0\\0.1\\0.15\\\end{matrix}\right)\\ &\left(\begin{matrix}\sigma_1\\\sigma_2\\\sigma_3\\\end{matrix}\right)=\left(\begin{matrix}0.1\\0.15\\0.2\\\end{matrix}\right)\\ &\left(\begin{matrix}\rho_{1,2}\\\rho_{1,3}\\\rho_{2,3}\\\end{matrix}\right)=\left(\begin{matrix}-0.5\\0.5\\-0.3\\\end{matrix}\right) \end{align} \]

最適保有比率$\boldsymbol{w}$を計算するために，まずは$\boldsymbol{\mu}$と$\boldsymbol{\Sigma}$の値を計算する． \[ \begin{align} \boldsymbol{\mu} & =\left(\begin{matrix}\mu_1\\\mu_2\\\mu_3\\\end{matrix}\right)=\left(\begin{matrix}0\\0.1\\0.15\\\end{matrix}\right)\\ \boldsymbol{\Sigma} & =\left(\begin{matrix}\sigma_1^2&\rho_{1,2}\sigma_1\sigma_2&\rho_{1,3}\sigma_1\sigma_3\\{\rho_{1,2}\sigma}_1\sigma_2&\sigma_2^2&{\rho_{2,3}\sigma}_2\sigma_3\\\rho_{1,3}\sigma_1\sigma_3&{\rho_{2,3}\sigma}_2\sigma_3&\sigma_3^2\\\end{matrix}\right) = \left(\begin{matrix}0.01&-0.0075&0.01\\-0.0075&0.0225&-0.009\\0.01&-0.009&0.04\\\end{matrix}\right) \end{align} \] 続いて，$\boldsymbol{w}$の公式に登場する$A$，$B$，$C$を定義通り計算すると， \[ \begin{align} A &\approx 1.44\\ B &\approx 11.20\\ C &\approx 282.29 \end{align} \] となるので，目標期待リターン$\mu_0$に対して，最適保有比率は以下のように書ける． \[ \begin{align} \boldsymbol{w} & = \boldsymbol{\Sigma}^{-1}\frac{\left(C\mu_0-B\right)\boldsymbol{\mu} + \left(A-B\mu_0\right)\boldsymbol{1_N}}{AC-B^2}\\ & = \frac{1}{AC - B^2}\boldsymbol{\Sigma}^{-1}\left(C\boldsymbol{\mu} - B \boldsymbol{1_N}\right)\mu_0+\frac{1}{AC-B^2}\boldsymbol{\Sigma}^{-1}\left(A \boldsymbol{1_N} - B\boldsymbol{\mu}\right)\\ &\approx\left(\begin{matrix}-7.43\\2.28\\5.15\\\end{matrix}\right)\mu_0+\left(\begin{matrix}0.91\\0.28\\-0.19\\\end{matrix}\right) \end{align} \]

（数値例終わり）

最後に，最適ポートフォリオの分散を$ \sigma_P^2= \boldsymbol{w^\prime} \boldsymbol{\Sigma} \boldsymbol{w}$で表すと，

\[ \begin{align} \sigma_P^2 = \frac{C \mu_0^2 - 2 B \mu_0 + A}{D} \end{align} \] と計算できる. ただし，$D = AC - B^2 $と置いた. さらに，この式は \[ \begin{align} \frac{\sigma_P^2}{(\sqrt{1/C})^2} - \frac{(\mu_0 - (B/C))^2}{(\sqrt{D} / C)^2} = 1 \end{align} \] と変形できるので，最適ポートフォリオが$ (\sigma_P, \mu_0) $平面において双曲線を描き，漸近線 \[ \begin{align} \mu_0 = \frac{B}{C} \pm \sqrt{\frac{D}{C}}\sigma_P \end{align} \] を持つことが確認できる．

S4.6 Rの実行環境の準備

本節ではR，及びRStudioのインストール方法を説明する．RStudioとは，Rのプログラミングをより簡単に行うためのアプリケーション（統合開発環境，IDE）である．したがって，Rによるプログラミングを行う上でRStudioのインストールは必須ではないが，RStudioは初学者向けの便利な機能を豊富に備えているため，同時にインストールしておくことをお薦めする．

なお，初学者向けにR，及びRStudioのインストール方法を丁寧に解説したサイトは数多く存在し，「R インストール方法 Windows」などと検索すれば，簡単に見つけることができる．以下の説明は，インストール環境の違いやバージョン変更などにより，必ずしもそのまま適用できない場合もありうるので，そうした外部サイトも適宜参照してほしい．

また，本サポートサイトS4.7節では，Posit Cloud（旧RStudio Cloud）やGoogle Colaboratoryを用いて，Rをクラウド上で実行する方法を説明する．しかし，無料での利用を前提にすると，これらのサイトには実行時間などの制約が存在する．したがって，まずは自身のコンピュータにR，及びRStudioをインストールを試み，それが何らかの理由でうまくいかない場合にこれらのサイトを利用するのが良いであろう．

Rのインストール
1. まずはCRAN (The Comprehensive R Archive Network)にアクセスする．
2. OS別にダウンロード先のリンクがあるので，Linux，Mac OS X，Windowsのいずれかを自身の環境に合わせて選択する．英語が苦手な場合は，Google翻訳などでサイト全体を日本語に翻訳するのも良いであろう．
3. リンク先の指示に従って，インストーラをダウンロードする．ここで言う，インストーラとは，Rのインストール及び設定を自動的に行なってくれるアプリケーションであり，Windowsの場合はexe，Mac OS Xの場合はpkgという拡張子がつく．Rのインストーラは，R-4.1.0-win.exeやR-4.0.5.pkgというように，ハイフンの後にバージョンを意味する数字を含む（具体的な数字は，その時点で利用可能なバージョンによって異なるので注意）．
4. ダウンロードしたインストーラをクリックして，Rをインストールする．途中，インストール先の指定等を求められるが，デフォルト選択のまま「次へ」を押していこう．
5. 無事にインストールが終了していれば，Rが利用可能になっているはずである．Windowsであればスタートメニュー，Mac OS XであればアプリケーションにRが追加されているか確認してみよう．このままそのアイコンをクリックしてRを実行することもできるが，以下では引き続き，RStudioもインストールして，そこからRを実行する方法を学んでいこう．
RStudioのインストール
1. RStudioの公式サイトから，インストーラをダウンロードする．RStudioにはデスクトップ版とサーバ版の二つが存在するが，ここではデスクトップ版を選択する．有料のプロ版含めて複数の選択肢があるが，無料のデスクトップ版を選択する．
2. インストーラを起動したら，先程と同様にインストール先の指定等を求められるが，デフォルト選択のまま「次へ」を押していく．
3. 無事にインストールが終了していれば，RStudioが利用可能になっているはずである．Windowsであればスタートメニュー，Mac OS XであればアプリケーションにRStudioが追加されているか確認してみよう．

S4.7 クラウド上でRを実行する方法

何らかの理由により，自身の環境にRやRStudioをインストールでいない場合，クラウド上でRを実行することも可能である．以下では，その例としてPosit Cloud（旧RStudio Cloud）とGoogle Colaboratoryを紹介する．

Posit Cloud

Posit Cloudは，RStudioをクラウド上で実行するサービスである．無料でユーザー登録すると，Webブラウザ上でRStudioを用いたプログラミングが可能となる．ただし，無料版では使用可能な時間やメモリなどに制約があるので，本格的なプログラミングを行うには有料版にアップグレードする必要がある．この点を除けば，ローカル環境でのRStudioと使い勝手はほとんど変わらず，例えば，install.packages()関数などを用いて必要なライブラリをインストールすることもできる．

図4.10: Posit Cloud上での実行例

Google Colaboratory

Google Colaboratoryは，Pythonによるプログラミングを主たる想定としているが，Rの実行も可能である．利用にはGoogleアカウントが必要なので，持っていない場合は作成しよう．自分でバックエンドをPythonからRに変更するのは面倒なので，このリンクをクリックして，Rが実行可能なノートブックを作成する．ノートブックとは，コードの入力と出力を同じウィンドウ内で行える対話的な環境のことで，セルに適当なコードを書き込んだ上で実行ボタンを押すと，結果がその下に表示されるはずである．

図4.11: Google Colaboratory上での実行例

S4.8 RStudio上で図表に日本語を挿入する方法

RStudio上で図表のタイトルや軸ラベルに日本語を入力すると，以下のように文字化けして表示されない場合がある．

# 連続複利による元本の増加を可視化

P <- 100 # 元本
R <- 0.1 # 金利
years <- seq(0, 10, by = 0.1) # 満期を表すベクトル (0, 0.1, 0.2, ..., 9.9, 10)

FV <- P * exp(R * years) # 各満期に対応する将来価値

plot(x = years, y = FV, type = "l", main = "連続複利の効果", xlab = "年数", ylab = "将来価値")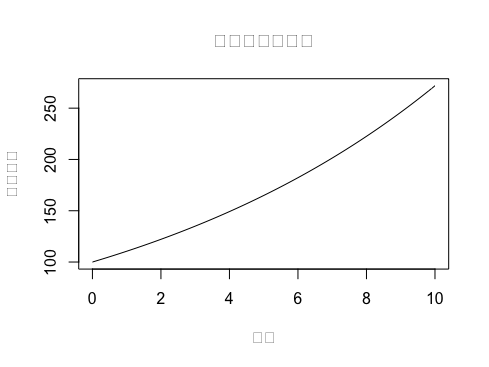

図4.12: タイトルや軸ラベルが文字化けした出力図

この問題を回避するため本文の図表は全て英語で統一したが，ここではその対処方法を解説しよう．日本語フォントが指定されていないことが原因の本質だが，フォント名はOSによって異なり環境依存であるため，対処が若干面倒である．

最も手っ取り早い方法の一つに，Rstudioを最新版へとアップデートした上，RstudioのメニューからPreferences > General > Graphicsを辿り，Graphic DeviceのBackendをAGGへと変更するというものである．それに変更するとき，raggパッケージのインストールが求められる場合があるので，その指示に従ってインストールを行う．install.packages("ragg")を実行してから，Backendの修正を行っても良いであろう．

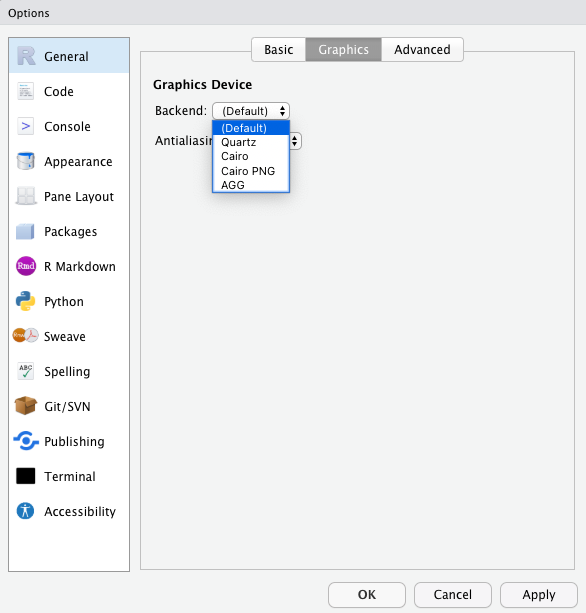
図4.13: Backendを変更する画面

それ以外には，fontregisterer というパッケージを使う方法もある．このパッケージはCRANに登録されていないので，githubから直接インストールする必要がある．そのために，まずはCRANからremotesパッケージをインストールした上で，以下のコードを実行して，fontregistererパッケージをインストールしよう．また，環境によってはsystemfontsパッケージを手動でインストールすることが求められる場合があるので，以下のコードではそれも同時に行っている．

install.packages("remotes")
install.packages("systemfonts")
remotes::install_github("Gedevan-Aleksizde/fontregisterer", repos = NULL)

その後の方法は，先ほどリンクした公式ページのREADME.mdファイルに詳しく説明されているので，そちらを参照してほしい．例えば，最近のMacOSの場合，ヒラギノ角ゴシック（ウェイトバリエーションはW4）はHiraginoSans-W4というフォント名で登録されている．このフォント名はOSによって異なり環境依存であるため，自身の環境に合わせた名称を使う必要がある．利用可能なフォントやそのフォント名を確認するためには，各自の環境でsystemfonts::system_fonts()を実行すれば良い．

par(family = "HiraginoSans-W4")
plot(x = years, y = FV, type = "l", main = "連続複利の効果", xlab = "年数", ylab = "将来価値")

図4.14: 文字化け解消後の出力図

S4.9 任意の線形ファクター・モデルに関する一般化

本文第7章では，FF3モデルを前提として，各銘柄の期待リターンや，リターン同士の共分散を推定した．ここでは，その議論が任意の線形ファクター・モデルに関して一般化できることを確認する．

$K$個のファクター${\{F}^k\}$ $(1, 2, \ldots, K)$を所与として，各銘柄の超過リターン$R_i^e$が以下の線形ファクター・モデルに従うとしよう $(i=1,2, \ldots, N)$． \[ R_i^e = \beta_i^1F^1 + \cdots + \beta_i^{K}F^{K} + \varepsilon_i \]

行列を用いると，各銘柄のリターンをまとめて表現できる． \[ \boldsymbol{R^e} = \boldsymbol{\beta F} + \boldsymbol{\varepsilon} \] ただし，各要素の定義は以下の通りである． \[ \begin{align} \boldsymbol{R^e} & = \left(\begin{matrix}R_1^e\\\vdots\\R_N^e\\\end{matrix}\right)\\ \boldsymbol{F} & = \left(\begin{matrix}F^1\\\vdots\\F^{K}\\\end{matrix}\right)\\ \boldsymbol{\beta} & =\ \left(\begin{matrix}\beta_1^1&\cdots&\beta_1^{K}\\\vdots&\ddots&\vdots\\\beta_N^1&\cdots&\beta_N^{K}\\\end{matrix}\right)\\ \boldsymbol{\varepsilon} & =\ \left(\begin{matrix}\varepsilon_1\\\vdots\\\varepsilon_N\\\end{matrix}\right) \end{align} \]

ここまで準備すると，本文第7章の議論が，任意の線形ファクター・モデルに関しても成立することが確認できる．まず，誤差項$\varepsilon_i$の期待値はゼロであるから，各銘柄の期待リターンは各ファクターの期待値の線形結合として表せる． \[ \mathbb{E}[\boldsymbol{R^e}] = \boldsymbol{\beta} \mathbb{E}[\boldsymbol{F}] \]

続いて，誤差項$\varepsilon_i$は各ファクターと無相関であるので，$\boldsymbol{R^e}$の分散共分散行列は次のように書ける． \[ \rm{Cov}[\boldsymbol{R^e}] = \boldsymbol{\beta} \rm{Cov}[\boldsymbol{F}]\boldsymbol{\beta^\prime} + \text{diag}(\rm{Var}[\boldsymbol{\varepsilon}]) \] ただし，$\text{diag}(\rm{Var}[\boldsymbol{\varepsilon}])$は$\varepsilon_i$の分散を対角要素とする対角行列である．

S4.10 会計情報ベースの株式価値評価モデル

本節では，本文312頁で紹介した残余利益モデルを始めとし，複数の会計情報ベースの株式価値評価モデルの導出過程やそれぞれのモデルの考え方を説明する⁷．

残余利益モデル

残余利益モデルとは，配当割引モデルを出発点として，それに会計上の基本制約式であるクリーン・サープラス関係を仮定することによって導出された価値評価モデルである．ここでは，そのモデルの導出過程について，順を追って説明していこう．まずは，任意の企業の時点0における株主価値$V_{0}$を配当割引モデル (Dividend Discount Model; DDM)によって表現するところから始めよう． \[ \begin{align} V_{0} & = \frac{\mathbb{E}[D_{1}]}{(1 + \widetilde{R})} + \frac{\mathbb{E}[D_{2}]}{(1 + \widetilde{R})^2} + \cdots \nonumber\\ & = \sum_{t = 1}^{\infty} \frac{\mathbb{E}[D_{t}]}{(1 + \widetilde{R})^{t}} \tag{4.2} \end{align} \] ただし，$\mathbb{E}[D_{t}]$は$t$期の総額ベースの配当の期待値（厳密には，時点0の情報集合に基づく条件付き期待値）を，$\widetilde{R}$は割引率を表すものとする．

次に，配当割引モデルを前提として，いくつかの仮定を置くことによって新たな価値評価モデルを導出するときに頻用されるゼロサム等式を紹介しよう．この段階では$y_{t}$の中身はさておき，次のような数列を考える． \[ \{y_{t}\}_{t = 0}^{\infty}: \quad y_{0}, \quad \frac{y_{1} - (1 + \widetilde{R})y_{0}}{(1 + \widetilde{R})}, \quad \frac{y_{2} - (1 + \widetilde{R})y_{1}}{(1 + \widetilde{R})^{2}}, \quad \cdots \]

次は，この数列の和を考えよう．$\lim_{T \rightarrow \infty}\frac{y_{T}}{(1 + \widetilde{R})^{T}} = 0$を仮定すれば，次式が成立する． \[ \begin{align*} & y_{0} + \frac{y_{1} - (1 + \widetilde{R})y_{0}}{(1 + \widetilde{R})} + \frac{y_{2} - (1 + \widetilde{R})y_{1}}{(1 + \widetilde{R})^{2}} \cdots \\ & \quad = (y_{0} - y_{0}) + \left(\frac{y_{1}}{1 + \widetilde{R}} - \frac{y_{1}}{1 + \widetilde{R}}\right) + \cdots\\ & \quad = 0 \end{align*} \]

今度は，$y_{t}$が確率変数であるとき，すなわち，$\{y_{t}\}_{t = 0}^{\infty}$が確率過程である場合を考えよう．期間$t$が進むにつれて利用可能な情報が増えていくとき，次式が成立する．なお，$\mathbb{E}[\cdot]$は，時点0の情報集合に基づく条件付き期待値を表し，$\lim_{T \rightarrow \infty}\mathbb{E}\left[\frac{y_{T}}{(1 + \widetilde{R})^{T}}\right] = 0$を仮定している． \[ \begin{align} &y_{0} + \frac{\mathbb{E}\left[y_{1} - (1 + \widetilde{R})y_{0}\right]}{(1 + \widetilde{R})} + \frac{\mathbb{E}\left[y_{2} - (1 + \widetilde{R})y_{1}\right]}{(1 + \widetilde{R})^{2}} \cdots \nonumber\\ & \quad = y_{0} + \sum_{t = 1}^{\infty} \frac{\mathbb{E}\left[y_{t} - (1 + \widetilde{R})y_{t-1}\right]}{(1 + \widetilde{R})^{t}} \nonumber\\ & \quad = 0 \tag{4.3} \end{align} \]

この式はゼロサム等式 (zero-sum equality)と呼ばれ，$y_{t}$に会計情報を代入することによって，配当割引モデルを会計情報ベースの価値評価モデルへと転換するのに役立てられる．試しに$y_{t}$に時点$t$の株主資本$\mathit{BE}_{t}$を代入してみよう．そのとき，(4.3)式は次のように変形される． \[ \begin{align} 0 = \mathit{BE}_{0} + \sum_{t = 1}^{\infty} \frac{\mathbb{E}\left[\mathit{BE}_{t} - (1 + \widetilde{R})\mathit{BE}_{t-1}\right]}{(1 + \widetilde{R})^{t}} \tag{4.4} \end{align} \]

こうして導出された(4.4)式と，(4.2)式で示した配当割引モデルとを足し合わせることによって，次式を導出することができる． \[ \begin{align} V_{0} = \mathit{BE}_{0} + \sum_{t = 1}^{\infty} \frac{\mathbb{E}\left[\mathit{BE}_{t} + D_{t} - (1 + \widetilde{R})\mathit{BE}_{t-1}\right]}{(1 + \widetilde{R})^{t}} \tag{4.5} \end{align} \]

ここで，本文311ページで示した会計上の基本制約式であるクリーン・サープラス関係を思い出そう．クリーン・サープラス関係を仮定すると，任意の期間 ($t = 1,2,\ldots$)について以下の式が成立する． \[ \begin{align} \underbrace{\mathit{BE}_{t-1}}_{\textbf{時点$t-1$の株主資本}} + \underbrace{X_{t}}_{\textbf{$t$期の当期純利益}} - \underbrace{D_{t}}_{\textbf{$t$期の配当}} & = \underbrace{\mathit{BE}_{t}}_{\textbf{時点$t$の株主資本}} \nonumber\\ \mathit{BE}_{t} - \mathit{BE}_{t-1} & = X_{t} - D_{t} \tag{4.6} \end{align} \]

先に導かれた(4.5)式にクリーン・サープラス関係を表す(4.6)式を代入してみよう． \[ \begin{align*} V_{0} & = \mathit{BE}_{0} + \sum_{t = 1}^{\infty} \frac{\mathbb{E}\left[\overbrace{\mathit{BE}_{t} - \mathit{BE}_{t-1}}^{X_{t} - D_{t}} + D_{t} - \widetilde{R} \times \mathit{BE}_{t-1}\right]}{(1 + \widetilde{R})^{t}} \\ & = \mathit{BE}_{0} + \sum_{t = 1}^{\infty} \frac{\mathbb{E}\left[X_{t} - \widetilde{R} \times \mathit{BE}_{t-1}\right]}{(1 + \widetilde{R})^{t}} \end{align*} \]

最後に，企業$i$を前提に上式を考え，また，本文(7.5)式を参考にしながら，企業$i$の$t$期の残余利益$X_{i,t}^{a}$を$X_{i,t} - \widetilde{R}_{i} \times \mathit{BE}_{i,t-1}$と定義すれば，本文312ページで示した残余利益モデルを導出することができる． \[ \begin{align*} V_{i,0} & = \mathit{BE}_{i,0} + \sum_{t = 1}^{\infty} \frac{\mathbb{E}\left[X_{i,t}^{a} \right]}{(1 + \widetilde{R}_{i})^{t}} \end{align*} \]

こうして，配当割引モデルと株主資本ベースのゼロサム等式，クリーン・サープラス関係を組み合わせることによって，B/Sの株主資本，P/Lの当期純利益といった会計情報を主たるインプットとした価値評価モデルが導出可能である．一方で，ゼロサム等式を工夫することで，クリーン・サープラス関係を仮定しない別の価値評価モデルを導出することもできる．以下では，その代表例である異常利益成長モデルの導出方法を概説しよう．

異常利益成長モデル

$y_{t}$に$t + 1$期の当期純利益$X_{t + 1}$を割引率$\widetilde{R}$で除したものを代入したゼロサム等式を考えてみよう．ここでは，$y_{0} = X_{1}/\widetilde{R}$となり，時点0の段階では実現していないので，期待値を取る必要があることに注意しよう． \[ \begin{align} 0 = \frac{\mathbb{E}\left[X_{1}\right]}{\widetilde{R}} + \sum_{t = 1}^{\infty} \frac{\mathbb{E}\left[\frac{X_{t+1}}{\widetilde{R}} - (1 + \widetilde{R})\frac{X_{t}}{\widetilde{R}}\right]}{(1 + \widetilde{R})^{t}} \tag{4.7} \end{align} \]

次に，こうして得られた(4.7)式と，(4.2)式で示した配当割引モデルとを足し合わせて整理すると， \[ \begin{align} V_{0} & = \frac{\mathbb{E}\left[X_{1}\right]}{\widetilde{R}} + \sum_{t = 1}^{\infty} \frac{\mathbb{E}\left[\frac{X_{t+1}}{\widetilde{R}} - (1 + \widetilde{R})\frac{X_{t}}{\widetilde{R}} + D_{t}\right]}{(1 + \widetilde{R})^{t}} \nonumber\\ & = \frac{\mathbb{E}\left[X_{1}\right]}{\widetilde{R}} + \sum_{t = 1}^{\infty} \frac{\mathbb{E}\left[\overbrace{\left(\frac{1}{\widetilde{R}}\right)\left( X_{t + 1} - \left((1 + \widetilde{R})X_{t} - \widetilde{R}D_{t}\right)\right)}^{\textbf{$Z_{t}$と定義}}\right]}{(1 + \widetilde{R})^{t}} \nonumber\\ & = \frac{\mathbb{E}\left[X_{1}\right]}{\widetilde{R}} + \sum_{t = 1}^{\infty} \frac{\mathbb{E}\left[Z_{t} \right]}{(1 + \widetilde{R})^{t}} \tag{4.8} \end{align} \]

が得られ，こうして導出された価値評価モデルは異常利益成長モデル (Abnormal Earnings Growth Model; AEGM)と呼ばれる．このモデルの特徴は，P/Lの当期純利益が主たるインプットになるという点である．AEGMによれば，時点0の株主価値$V_{0}$は，(1) 第一項に相当する1期先の期待利益$\mathbb{E}[X_{1}]$を割引率$\widetilde{R}$で割った部分と(2) 第二項に相当する$Z_{t}$の現在価値合計に分解される．以下ではそれぞの項の持つ経済的な意味を解説していこう．

AEGMでは，まず，時点0の株主資本$\mathit{BE}_{t}$から派生する投資の成果である1期先の期待利益$\mathbb{E}[X_{1}]$を考え，それと同額の利益がその後も毎期永続すると暫定的に仮定し，その現在価値が株主価値の一部を構成すると見なす．この仮定のもとでは，S4.2節の等比数列の和の公式を利用して， \[ \frac{\mathbb{E}[X_{1}]}{1 + \widetilde{R}} + \frac{\mathbb{E}[X_{1}]}{(1 + \widetilde{R})^2} + \cdots = \frac{\mathbb{E}[X_{1}]}{\widetilde{R}} \]

が得られ，これはAEGMの第一項そのものである．その第一項を与件として，更に追加・削減される株主価値があるとすれば，それは第二項に当たる将来の$\mathbb{E}[Z_{t}]$の流列を現在価値に割り引いたものであるというのがAEGMによる価値評価である．そこで，次に$Z_{t}$の経済的意味を考えていこう．それを説明する前に，理解しておきたいのが，資本化という考え方である．いま，次の図の通り，期首と期末の二時点を考え，期末に得られるであろう期待キャッシュフローが105，要求収益率が5%とすれば，期首時点の価値は次のように求めることができる（本文2.1節参照）．

\[ \text{期首時点の価値} = \frac{100 + 5}{1 + 5\%} = 100 \]

一方，期待キャッシュフロー105から投資元本100を抜いた期待ペイオフ5を要求収益率5%で除すことによっても，期首時点の価値を求めることができる． \[ \text{期首時点の価値} = \frac{5}{5\%} = 100 \]

すなわち，投資期間中における投資元本の増殖分に相当するペイオフの期待値を要求収益率で除すことによっても期首時点の価値は計算可能なのである．このように期待ペイオフを要求収益率で除し，価値へと変換する行為を資本化 (capitalizing)と呼ぶ．この事実を踏まえ，$Z_{t}$の中身を改めて見てみると， \[ \begin{align} Z_{t} & = \left(\frac{1}{\widetilde{R}}\right)\left( X_{t + 1} - \left((1 + \widetilde{R})X_{t} - \widetilde{R}D_{t}\right)\right) \nonumber\\ & = \frac{X_{t + 1} - \left((1 + \widetilde{R})X_{t} - \widetilde{R}D_{t}\right)}{\widetilde{R}} \tag{4.9} \end{align} \]

となり，分子に相当するペイオフを期首時点の価値へと資本化したのが，$Z_{t}$であることが分かる．分子の$X_{t + 1} - \left((1 + \widetilde{R})X_{t} - \widetilde{R}D_{t}\right)$は，$t + 1$期の異常利益成長 (Abnormal Earnings Growth; AEG)と呼ばれる．その理由は，$t$期の利益$X_{t}$を与件として，投資家が最低限要求する$t+1$期の利益は$(1 + \widetilde{R})X_{t} - \widetilde{R}D_{t}$だからである．投資家は，$X_{t}$の利益を稼ぐ企業に対して，翌$t+1$期には自分たちが最低限要求する収益率で利益が成長し，$(1 + \widetilde{R})X_{t}$の利益を稼ぐことを望むはずである．一方で，$t$期には$X_{t}$の利益から$D_{t}$の配分を既に受けているため，$D_{t}$を要求収益率$\widetilde{R}$で運用した額までの成長は望まない．したがって，投資家が$t + 1$期に最低限望む正常利益 (required normal earnings)は，$(1 + \widetilde{R})X_{t}$から$\widetilde{R}D_{t}$を控除した$(1 + \widetilde{R})X_{t} - \widetilde{R}D_{t}$である．その正常利益を超える利益を$t + 1$期に獲得することができるならば，$t + 1$期には正の異常利益成長があったと見なし，それが期待できる企業は株主から高く評価される．その結果，時点0の株主価値はより高くなるのである．$t + 1$期の異常利益成長$\mathit{AEG}_{t+1}$は，次のように定義される． \[ \underbrace{\mathit{AEG}_{t+1}}_{\textbf{$t + 1$期の異常利益成長}} = \underbrace{X_{t + 1}}_{\textbf{$t+1$期の利益}} - \underbrace{\left((1 + \widetilde{R})X_{t} - \widetilde{R}D_{t}\right)}_{\textbf{$t$期の利益と配当を与件とした$t + 1$期の正常利益}} \]

ただし，こうして計算された$t + 1$期の異常利益成長は，価値ではなく，あくまで利益の異常な増殖分（あるいは，減衰分）にしか過ぎない．そこで，資本化の手続きによって価値へと変換する必要がある．それが，$Z_t$である．すなわち，$Z_{t}$とは，$t+1$期の異常利益成長$\mathit{AEG}_{t+1}$を，$t+1$期首，すなわち，時点$t$の価値へと変換したものである． \[ Z_{t} = \frac{\mathit{AEG}_{t + 1}}{\widetilde{R}} \] ここまでの説明を概要図として要約したのが，以下である．

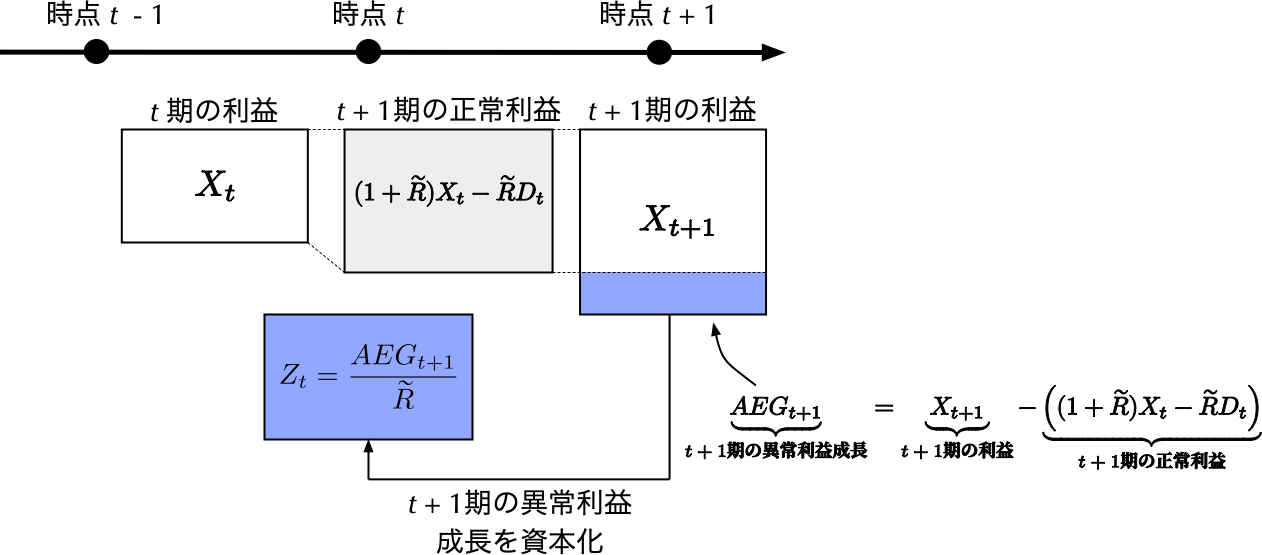
こうして定義された$Z_{t}$の期待値$\mathbb{E}[Z_{t}]$ ($t = 1, 2, \ldots$)，すなわち，資本化された将来の期待異常利益成長の現在価値合計$\sum_{t = 1}^{\infty}\mathbb{E}[Z_{t}]/(1 + \widetilde{R})^{t}$が，時点0の株主価値に加算・減算されるとことになる．その現在価値合計は，ファイナンスの教科書（例えば，Brealey, Myers, and Allen (2020)^[1]を参照）でしばしば登場する成長機会のNPV (net present value of growth opportunities; PVGO)を定式化したものと捉えることができる．以上をまとめると，AEGMとは，時点0の株主価値$V_{0}$を次の図のように評価する価値評価モデルである．

Ohlson and Jüettnerモデル

AEGMの導出の際に登場した$Z_{t}$について，毎期一定の割合$G$で成長するとし，数列$\{Z_{t}\}_{t = 1}^{\infty}$が，次の関係を満たすと仮定しよう． \[ \begin{align} Z_{t + 1} &= (1 + G)Z_{t}~~~(t = 1, 2, \ldots) \\ & \text{where } 1 < (1 + G) < (1 + \widetilde{R}) \quad \text{and} \quad Z_{t} > 0 \end{align} \]

そのとき，時点0の株主価値$V_{0}$は，次のように表される． \[ \begin{align} V_{0} & = \frac{\mathbb{E}\left[X_{1}\right]}{\widetilde{R}} + \frac{\mathbb{E}[Z_{1}]}{1 + \widetilde{R}} + \frac{\mathbb{E}[(1 + G)Z_{1}]}{(1 + \widetilde{R})^2} + \ldots\\ &= \frac{\mathbb{E}\left[X_{1}\right]}{\widetilde{R}} + \frac{\mathbb{E}[Z_{1}]}{\widetilde{R} - G} \\ & = \frac{\mathbb{E}\left[X_{1}\right]}{\widetilde{R}} + \frac{\mathbb{E}\left[X_{2} -\left((1 + \widetilde{R})X_{1} - \widetilde{R}D_{1}\right) \right]}{\widetilde{R}(\widetilde{R} - G)} \end{align} \]

このように導かれた新たな価値評価モデルはOhlson and Jüettner-Nauroth (2005)^[5]によって提案され，それにちなんでOhlson and JüettnerモデルやOJモデルと呼ばれる．このモデルは，一期先の利益$X_{1}$や配当$D_{1}$，二期先の利益$X_{2}$の期待値など，アナリストや経営者による予想を通じて，どの企業でも比較的入手が容易なインプットのみを必要とし，また，あとは正確な成長率$G$さえ見積ることができれば良いので，他のモデルに比べて，相対的に少ないインプットで価値評価を行えるという点に特徴がある．Ohlson and Jüettnerモデルは，株主価値を評価する以外にも，本文のコラム7.2（309頁）で紹介した潜在資本コストの推定に活用されることもある（例えば，Gode and Mohanram (2003)^[3]を参照）．

クリーン・サープラス関係を仮定した異常利益成長モデル

残余利益モデルとは異なり，AEGMやOhlson and Jüettnerモデルはクリーン・サープラス関係を仮定せずに導出された価値評価モデルである．ただし，残余利益モデルと同様，AEGMについても，クリーン・サープラス関係を仮定することで，モデル内に登場する配当$D_{t}$を消し去ることができ，B/Sの株主資本とP/Lの当期純利益のみがインプットとなる新たな価値評価モデルが導出可能である．そこで本小節では，クリーン・サープラス関係を仮定した場合のAEGMを導出し，その価値評価モデルの経済的意味を解説していこう．

まずは，(4.6)式で示したクリーン・サープラス関係を$D_{t}$について解き，以下のように変形しよう． \[ D_{t} = -\mathit{BE}_{t} + \mathit{BE}_{t-1} + X_{t} \]

この式を(4.9)式に代入し，整理すると， \[ \begin{align} Z_{t} & = \frac{X_{t + 1} - \left((1 + \widetilde{R})X_{t} - \widetilde{R}(-\mathit{BE}_{t} + \mathit{BE}_{t-1} + X_{t})\right)}{\widetilde{R}} \nonumber\\ & = \frac{\overbrace{\left( X_{t + 1} - \widetilde{R} \times \mathit{BE}_{t}\right)}^{\textbf{$t + 1$期の残余利益}} - \overbrace{\left( X_{t} - \widetilde{R} \times \mathit{BE}_{t - 1}\right)}^{\textbf{$t$期の残余利益}}}{\widetilde{R}} \nonumber\\ & = \frac{\overbrace{X_{t+1}^{a} - X_{t}^{a}}^{\textbf{$t$期から$t+1$期にかけての残余利益変化}}}{\widetilde{R}} \end{align} \]

が得られる．当初，資本化された異常利益成長を表していた$Z_{t}$は，クリーン・サープラス関係を仮定することで，残余利益の期間変化を資本化したものへと変形することができる．こうして得られた式を，(4.8)式で示したAEGMに代入することによって，クリーン・サープラス関係を仮定した場合のAEGMが得られるのである． \[ V_{0} = \frac{\mathbb{E}\left[X_{1}\right]}{\widetilde{R}} + \underbrace{\sum_{t = 1}^{\infty} \frac{\mathbb{E}\left[ (X_{t+1}^{a} - X_{t}^{a})/\widetilde{R} \right]}{(1 + \widetilde{R})^{t}}}_{\textbf{資本化された期待残余利益変化の現在価値合計}} \] 第二項は，資本化された期待残余利益変化の現在価値合計を表し，このモデルは，残余利益の成長機会が，価値創造の要の一つになることを示唆している．

S3 本書のコード一覧

S5 サポートサイト内の参考文献

	事業利益	純金融費用	当期純利益
① 税引前	\(190\)	\(55\)	\(135\)
② 税金 (\(=\) ① \(\times\) 40%)	\(76\)	\(22\)	\(54\)
税引後 (\(=\) ① \(-\) ②)	\(\underbrace{114}_{OX_{t}}\)	\(\underbrace{33}_{NFE_{t}}\)	\(\underbrace{81}_{X_{t}}\)

笠原・村宮 (2022)『実証会計・ファイナンス - Rによる財務・株式データの分析』サポートサイト